- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-02-01 14:12.
- Naposledy změněno 2025-01-23 12:14.
Matematiku se může naučit každý, ať už je ve škole na vyšším stupni, nebo chce jen znovu zdokonalit základy. Po diskusi o tom, jak být dobrým žákem v matematice, vás tento článek naučí základní matematické pokroky a poskytne vám základní prvky, které se budete muset naučit v každé praxi. Tento článek pak bude diskutovat o základech učení aritmetiky, což pomůže jak dětem na základní škole, tak všem, kteří se chtějí naučit základy tohoto vědního oboru.
Krok
Část 1 ze 6: Klíče k tomu, stát se dobrým studentem matematiky

Krok 1. Objevte se ve třídě
Když zmeškáte hodinu, měli byste se naučit pojmy od spolužáků nebo z učebnice. Nikdy od přítele nedostanete textové shrnutí stejně jako od svého učitele.
- Přijď do třídy včas. Místo toho přijďte o něco dříve a otevřete si notebook na správném místě, otevřete učebnici a vytáhněte kalkulačku, abyste byli připraveni začít, když je váš učitel připraven učit.
- Pouze záškoláci, pokud jste nemocní. Pokud vám hodina opravdu chybí, požádejte své spolužáky, aby zjistili, o čem učitel mluvil a jaké domácí úkoly dostal.

Krok 2. Spolupracujte se svým učitelem
Pokud váš učitel pracuje na problému před třídou, pracujte s učitelem tak, že problém vyřešíte ve svém poznámkovém bloku.
- Ujistěte se, že jsou vaše poznámky jasné a snadno čitelné. Nepište jen otázky. Zapište si také vše, co vám učitel řekne, což může zlepšit vaše chápání vysvětlovaných pojmů.
- Vyplňte ukázkové otázky, které vám položil váš učitel. Když učitel při práci chodí po třídě, odpovězte na položené otázky.
- Zúčastněte se, když učitel vyřeší problém. Nečekejte, až vám učitel zavolá. Nabídněte odpověď, pokud znáte odpověď, a zvedněte ruku, abyste položili otázku, pokud si nejste jisti učeným materiálem.

Krok 3. Udělejte si domácí úkol ve stejný den, kdy máte domácí úkol
Pokud si uděláte domácí úkol ve stejný den, koncept je stále čerstvý ve vaší mysli. Někdy není možné dokončit domácí úkol ve stejný den. Než půjdete do třídy, ujistěte se, že máte hotové domácí úkoly.

Krok 4. Pokud potřebujete pomoc, pracujte mimo třídu
Navštěvujte svého učitele o přestávkách nebo v úředních hodinách.
- Pokud máte ve škole matematické centrum, zjistěte si jeho otevírací dobu a požádejte o pomoc.
- Připojte se ke studijní skupině. Dobrá studijní skupina se obvykle skládá ze 4 nebo 5 lidí s různými úrovněmi schopností. Pokud jste studentem matematiky „C“, připojte se ke skupině 2 nebo 3 studentů s hodnocením „A“nebo „B“, abyste mohli zlepšit své dovednosti. Vyhněte se připojení ke skupině studentů, jejichž známky jsou nižší než vaše.
Část 2 ze 6: Učení matematiky ve škole

Krok 1. Začněte s aritmetikou
Ve většině škol se studenti učí aritmetice na základní škole. Aritmetika pokrývá základy sčítání, odčítání, násobení a dělení.
- Cvičte otázky. Dělat aritmetické problémy znovu a znovu je nejlepší způsob, jak si správně zapamatovat základy. Hledejte software, který vám poskytne širokou škálu různých matematických problémů, se kterými budete pracovat. Hledejte také problémy s časovými rámci, abyste zvýšili rychlost.
- Můžete také najít aritmetické problémy online a aritmetické aplikace si můžete stáhnout do svého mobilního zařízení.

Krok 2. Pokračujte s pre-algebrou
Toto cvičení vám poskytne základní prvky, které budete později potřebovat k řešení problémů s algebrou.
- Přečtěte si o zlomcích a desetinných číslech. Naučíte se sčítat, odčítat, násobit a dělit zlomky a desetinná místa. Pokud jde o zlomky, naučíte se odčítat zlomky a překládat kombinovaná čísla. Pokud jde o desetinná místa, porozumíte místním hodnotám a v problémech s příběhem budete moci používat desetinná místa.
- Přečtěte si o poměrech, poměrech a procentech. Tyto koncepty vám pomohou naučit se porovnávat.
- Představte se základní geometrii. Naučíte se 3D tvary a koncepty. Naučíte se také pojmy jako plocha, obvod, objem a povrch a také informace o rovnoběžných a kolmých čarách a úhlech.
- Pochopte některé základní statistiky. V pre-algebře váš úvod do statistik obecně zahrnuje vizuály, jako jsou grafy, bodové grafy, grafy razítek a histogramy.
- Naučte se základy algebry. To zahrnuje koncepty, jako je řešení jednoduchých rovnic obsahujících proměnné, poznávání vlastností, jako je distribuční vlastnost, kreslení jednoduchých rovnic a řešení nerovností.
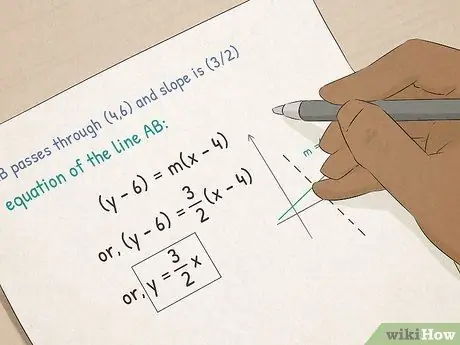
Krok 3. Pokrok v algebře I
Ve svém prvním ročníku algebry se seznámíte se základními symboly obsaženými v algebře. Naučíte se také:
- Řešte rovnice a nerovnice obsahující proměnné. Naučíte se, jak tyto problémy řešit na papíře a jak je řešit pomocí obrázků.
- Vyřešte problémy s příběhem. Budete překvapeni, s jak mnoha každodenními problémy se v budoucnu setkáte a které vyžadují schopnost řešit problémy s algebraickým příběhem. Pomocí algebry byste například zjistili úrokovou sazbu, kterou vyděláte na svém bankovním účtu nebo investici. Pomocí algebry můžete také zjistit, jak dlouho byste měli cestovat, podle rychlosti vašeho auta.
- Práce s exponenty. Když začnete řešit polynomiální rovnice (výrazy, které obsahují čísla a proměnné), pochopíte, jak používat exponenty. To bude pravděpodobně zahrnovat cvičení s vědeckou notací. Jakmile zvládnete exponenty, můžete se naučit sčítat, odčítat, násobit a dělit polynomické výrazy.
- Vyřešte odmocniny a odmocniny. Když zvládnete toto téma, budete si moci zapamatovat čtverce mnoha čísel. Budete také moci pracovat s rovnicemi, které mají odmocniny.
- Pochopte funkce a grafy. V algebře se dozvíte o grafických rovnicích. Naučíte se, jak vypočítat sklon čáry, jak vložit rovnici do tvaru bodového sklonu a jak vypočítat x-a-y řez čáry pomocí formuláře pro zachycení sklonu.
- Zjistěte soustavu rovnic. Někdy dostanete 2 různé rovnice s proměnnými xay a pro obě rovnice musíte vyřešit x nebo y. Naštěstí se naučíte spoustu triků pro řešení těchto rovnic, včetně grafů, substitucí a sčítání.

Krok 4. Studujte geometrii
V geometrii se seznámíte s vlastnostmi čar, segmentů, úhlů a tvarů.
- Zapamatujete si řadu vět a důsledků, které vám pomohou porozumět pravidlům geometrie.
- Dozvíte se, jak vypočítat plochu kruhu, jak používat Pythagorovu větu a jak najít vztah mezi úhly a stranami speciálního trojúhelníku.
- V budoucích standardizovaných testech, jako jsou SAT, ACT a GRE, uvidíte mnoho otázek týkajících se geometrie.
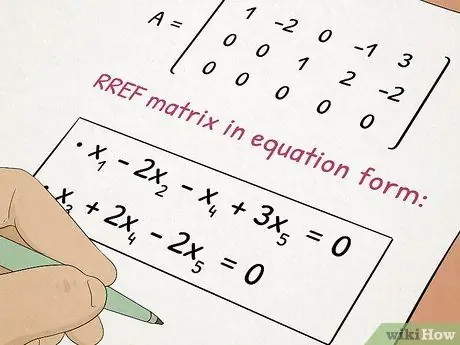
Krok 5. Vezměte třídu Algebra II
Algebra II navazuje na koncepty, které jste se naučili v Algebře I, a přidáváte do komplexních témat, jako jsou kvadratické rovnice a matice.
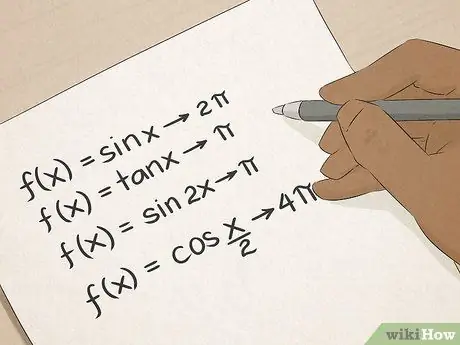
Krok 6. Zvládněte trigonometrii
Znáte goniometrické výrazy: sinus, kosinus, tangens atd. Trigonometrie vás naučí mnoho praktických způsobů výpočtu úhlů a délek čar a tyto dovednosti budou neocenitelné pro lidi pracující ve stavebnictví, architektuře, strojírenství nebo geodézii.
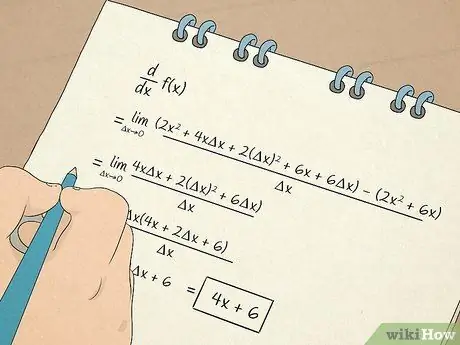
Krok 7. Proveďte výpočty počtu
Kalkul může znít zastrašující, ale je to skvělý nástroj k pochopení chování čísel nebo světa kolem vás.
- Calculus vás naučí funkce a limity. Uvidíte chování čísel užitečných funkcí včetně e^x a logaritmických funkcí.
- Naučíte se také počítat a pracovat s deriváty. První derivace vám poskytne informace na základě sklonu tečné přímky k rovnici. Například derivát vám řekne, jakou rychlostí se něco mění v nelineární situaci. Druhá derivace vám řekne, zda se funkce v určitém intervalu zvyšuje nebo snižuje, takže můžete určit konkávnost funkce.
- Integrály vás naučí vypočítat plochu pod křivkou i její objem.
- Kalkul na střední škole obecně končí posloupnostmi a posloupnostmi. Přestože studenti neuvidí mnoho aplikací pro obvody, obvody jsou důležité pro ty, kteří studují diferenciální rovnice.
Část 3 ze 6: Základy matematiky-hlavní doplnění

Krok 1. Začněte fakty „+1“
Přidáním 1 k číslu se dostanete na nejvyšší číslo na číselném řádku. Například 2 + 1 = 3.
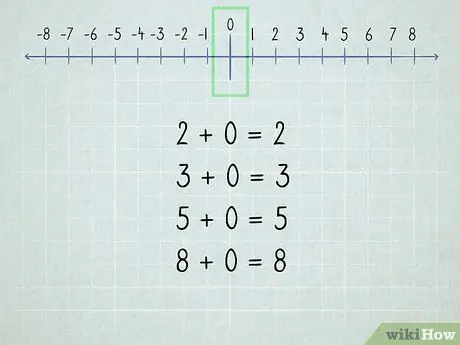
Krok 2. Pochopte nulu
Všechna čísla přidaná k nule jsou stejná čísla, protože „nula“znamená „žádné“.

Krok 3. Naučte se dvojitá čísla
Více čísel je problém, který zahrnuje sčítání dvou stejných čísel. Například 3 + 3 = 6 je příkladem rovnice zahrnující více čísel.

Krok 4. Pomocí mapování se dozvíte o dalších řešeních přidávání
V níže uvedeném příkladu se naučíte mapováním toho, co se stane, když přidáte 3 k 5, 2 a 1. Zkuste sami problém „přidat o 2“.

Krok 5. Pokračujte, dokud číslo nepřesáhne 10
Naučte se sčítat 3 čísla dohromady, abyste získali číslo větší než 10.
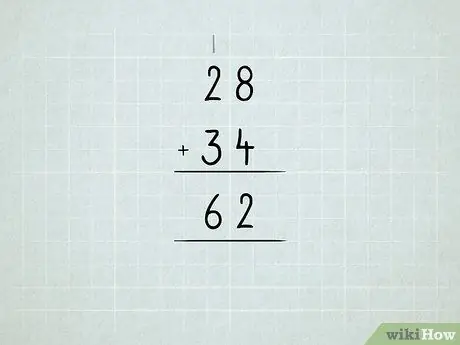
Krok 6. Sečtěte větší čísla
Přečtěte si o přeskupování jednotek na desítky, desítky na stovky atd.
- Nejprve sečtěte čísla v pravém sloupci. 8 + 4 = 12, což znamená, že máte 1 číslo 10 a 2 číslo 1. Do sloupce jednotek napište číslo 2.
-
Do sloupce desítek napište číslo 1.
-
Sečtěte sloupec desítek jako celek.
Část 4 ze 6: Matematické základy-strategie redukce

Krok 1. Začněte „zpět o 1 číslici
„Odečtením 1 od čísla se dostanete zpět o 1 číslo. Například 4 - 1 = 3.

Krok 2. Naučte se odečíst dvojitá čísla
Například sečtete čísla 5 + 5 a dostanete 10. Stačí napsat rovnici zpět a dostanete 10 - 5 = 5.
- Pokud 5 + 5 = 10, pak 10 - 5 = 5.
-
Pokud 2 + 2 = 4, pak 4 - 2 = 2.

Krok 3. Zapamatujte si rodinu faktů
Jako příklad:
- 3 + 1 = 4
- 1 + 3 = 4
- 4 - 1 = 3
- 4 - 3 = 1

Krok 4. Najděte chybějící čísla
Například _ + 1 = 6 (odpověď je 5).

Krok 5. Zapamatujte si fakt odečtení na 20

Krok 6. Procvičte si odčítání 1místných čísel od 2místných čísel bez vypůjčování
Odečtěte čísla ve sloupci jedničky a snižte čísla ve sloupci desítky.
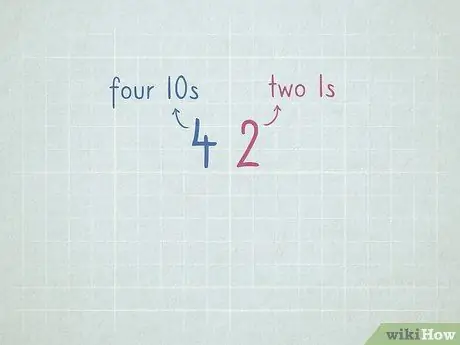
Krok 7. Procvičte si hodnotu místa, abyste se připravili na odčítání výpůjčkami
- 32 = 3 čísla 10 a 2 čísla 1.
- 64 = 6 čísel 10 a 4 čísla 1.
- 96 = _ číslo 10 a _ číslo 1.
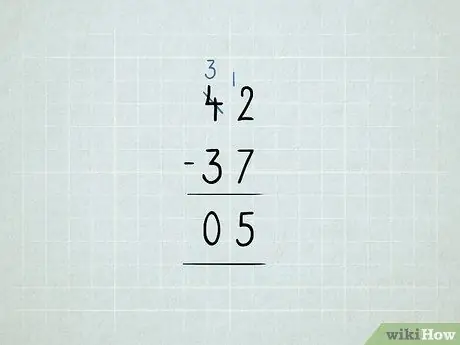
Krok 8. Odečtěte výpůjčkou
- Chcete odečíst 42 - 37. Začnete tím, že se pokusíte odečíst 2 - 7 ve sloupci jednotek. Ukázalo se, že to nefungovalo!
-
Půjčte si číslo 10 ze sloupce desítek a umístěte jej do sloupce ty. Nyní máte 3 10 namísto 4 10. Nyní máte 12 1 místo 2 1.
-
Nejprve odečtěte sloupec jednotek: 12 - 7 = 5. Poté zkontrolujte sloupec desítek. Protože 3 - 3 = 0, nemusíte zapisovat číslo 0. Vaše odpověď je 5.
Část 5 ze 6: Základy matematiky-hlavní násobení

Krok 1. Začněte číslem 1 a číslem 0
Všechna čísla, která jsou vynásobena 1, jsou stejná jako samotné číslo. Libovolné číslo vynásobené 0 se rovná nule.

Krok 2. Zapamatujte si multiplikační tabulku

Krok 3. Cvičte s problémy s násobením jedné číslice

Krok 4. Vynásobte 2místné číslo 1místným číslem
- Vynásobte číslo vpravo dole číslem vpravo nahoře.
-
Vynásobte číslo vpravo dole číslem vlevo nahoře.
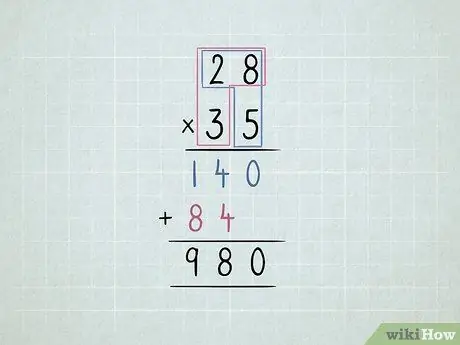
Krok 5. Vynásobte 2 2místná čísla
- Vynásobte číslo vpravo dole číslem vpravo nahoře a poté číslem vlevo nahoře.
-
Přesuňte druhý řádek o jednu číslici doleva.
- Vynásobte číslo vlevo dole číslem vpravo nahoře a poté číslem vlevo nahoře.
-
Sečtěte všechny sloupce.
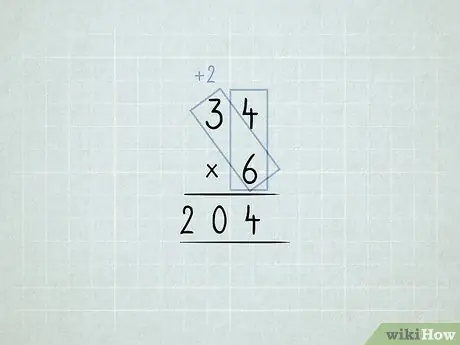
Krok 6. Násobte a přeskupte sloupce
- Chcete znásobit 34 x 6. Začnete vynásobením sloupce jednotek (4 x 6), ale ve sloupci ty nemůžete mít 24 1 s.
-
Uložte 4 1 s do sloupce jednotek. Přesuňte 2 10 s do sloupce desítek.
-
Vynásobte 6 x 3, což se rovná 18. Přidejte 2, které jste přesunuli, což se rovná 20.
Část 6 ze 6: Matematické základy-odhalení problémů divize

Krok 1. Přemýšlejte o rozdělení na rozdíl od násobení
#* Pokud 4 x 4 = 16, pak 16/4 = 4.
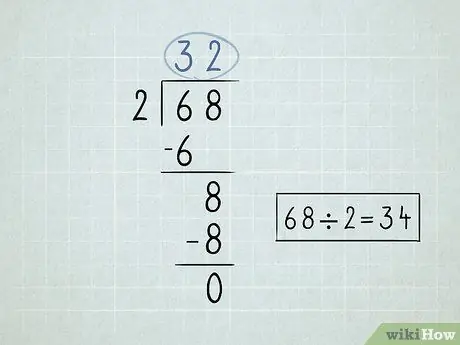
Krok 2. Zapište si problém s rozdělením
- Vydělte číslo nalevo od symbolu rozdělení nebo dělitele prvním číslem pod symbolem dělitele. Protože 6 /2 = 3, napsali byste číslo 3 nad symbol rozdělení.
-
Vynásobte číslo nad symbolem dělení dělitelem. Výsledek přeneste dolů na konec prvního čísla pod symbol rozdělení. Protože 3 x 2 = 6, pak číslo 6 snížíte.
- Odečtěte 2 zapsaná čísla. 6 - 6 = 0. Můžete nechat 0 prázdné, protože obecně nezačínáte čísly 0.
-
Snižte druhé číslo, které je pod symbolem rozdělení.
- Rozdělte číslo, které svrhnete dělitelem. V tomto případě 8 /2 = 4. Napište číslo 4 nad symbol rozdělení.
-
Vynásobte pravé horní číslo dělitelem a snižte číslo. 4 x 2 = 8.
-
Odečtěte tato čísla. Konečné odečtení vrátí nulu, což znamená, že jste problém vyřešili. 68 x 2 = 34.

Krok 3. Vypočítejte také zbytek
Někteří z dělitelů nejsou plně rozděleni na jiná čísla. Pokud jste dokončili poslední odčítání a nemáte žádná další čísla, která byste mohli odvodit, pak poslední číslo je zbytek.






