- Autor Jason Gerald [email protected].
- Public 2023-12-16 11:01.
- Naposledy změněno 2025-01-23 12:14.
Desetinná (základní desetina) číselná soustava má pro každou pozici čísla deset možných hodnot (0, 1, 2, 3, 4, 5, 6, 7, 8 nebo 9). Naproti tomu binární (základní dvě) číselná soustava má pouze dvě možné hodnoty reprezentované 0 a 1 pro každou číselnou pozici. Protože binární číselná soustava je interním jazykem elektronických počítačů, seriózní počítačoví programátoři vědí, jak převést z desítkové na binární číselnou soustavu. Postupujte podle těchto jednoduchých kroků a také jak tuto konverzi zvládnout.
Krok
Metoda 1 ze 2: Krátké rozdělení dvěma se zbytkem

Krok 1. Určete problém
V tomto případě převeďme desetinné číslo 15610 být binární číslo. Do symbolu převráceného dělení napište desetinné číslo jako číslo, které se má rozdělit. Napište základ cílového číselného systému (v tomto případě „2“pro binární) jako dělič mimo křivku symbolu dělení.
- Tato metoda je mnohem snáze pochopitelná při kreslení na papír a mnohem snazší pro začátečníky, protože dělí pouze dvěma.
- Abyste předešli nejasnostem před a po převodu, zapište si pro každé číslo základní číslo číselné soustavy, kterou vypočítáváte, jako dolní index (malá písmena psaná běžnými písmeny jako rozlišovací znak). V tomto případě bude mít desetinné číslo dolní index 10 a binární číslo bude mít dolní index 2.

Krok 2. Proveďte rozdělení
Pod symbol dlouhého dělení napište celočíselnou odpověď (kvocient) a napravo od děleného čísla napište zbytek (0 nebo 1).
Protože dělíme dvěma, když je dělené číslo sudé číslo, pak zbytek je 0, a když je dělené číslo liché, pak zbytek je 1

Krok 3. Pokračujte v dělení, dokud nedosáhne nuly
Pokračujte z kopce, vydělte každý nový podíl dvěma a zapište zbytek napravo od každého děleného čísla. Zastavte, když je kvocient nula.

Krok 4. Zapište si nové binární číslo
Počínaje od nejnižšího zbývajícího čísla si přečtěte pořadí zbytku ve vzestupném pořadí nahoru. V tomto případě byste měli získat výsledek 10011100. Toto je binární ekvivalent desetinného čísla 156. Nebo, pokud je napsáno s jeho základním indexem číselné báze: 15610 = 100111002.
Tuto metodu lze upravit tak, aby převáděla z desítkové základny na libovolnou číselnou základnu. Dělitel je 2, protože základem cílového číselného systému je základna 2 (binární). Pokud je základem cílového číselného systému jiná základna, nahraďte číslo 2 v této metodě příslušným základním číslem. Pokud je například cílová základna základna 9, nahraďte číslo základny 2 číslem 9. Konečný výsledek bude přímo ve formě čísla cílové základny
Metoda 2 ze 2: Odvození síly dvou a odčítání

Krok 1. Začněte vytvořením tabulky
Zapište si mocniny dvou základních čísel do „základny 2 tabulky“zprava doleva. Začněte ve 20, napište jej jako „1“. U každé pozice zvyšte hodnost o 1. Vyplňujte tabulku, dokud nezískáte číslo, které je nejblíže číslu desítkové soustavy, kterou vypočítáváte. V tomto případě převeďme desetinné číslo 15610 být binární číslo.

Krok 2. Najděte číslo s největší mocí základního čísla 2
Z tabulky vyberte největší číslo, které je stejné nebo menší než číslo, které má být převedeno. Číslo 128 je číslo s největší mocninou základního čísla 2 a je také menší než 156, proto pod toto pole v tabulce napište číslo „1“, kde je největší číslo z tabulky vlevo (viz tabulka na obrázku výše). Poté odečtěte 128 z počátečního čísla, získáte: 156 - 128 = 28.
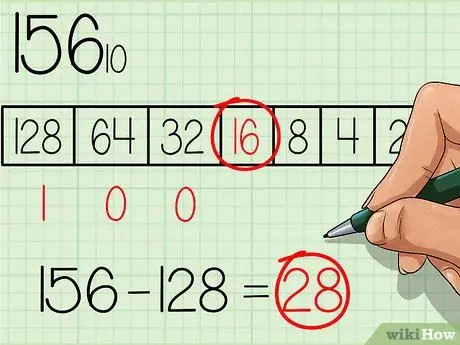
Krok 3. Pokračujte na další menší výkon v tabulce
Pomocí nového čísla (28) pokračujte v tabulce zleva doprava a kontrolujte, zda jsou čísla stejná nebo menší než nové číslo. Číslo 64 není menší než 28, proto do pole 64 zadejte číslo „0“. Pokračujte, dokud nenajdete číslo, které je rovné nebo menší než 28.
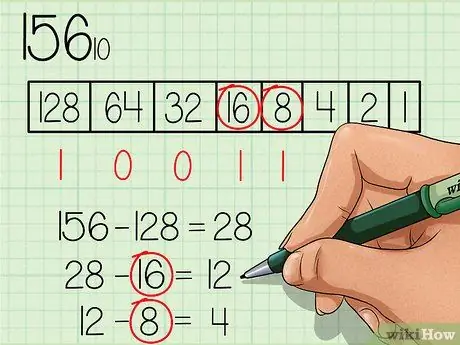
Krok 4. Odečtěte nepřetržitě každé číslo, které se rovná novému číslu nebo je menší, a příslušné číslo označte pod rámečkem číslem „1“
Číslo 16 je menší než 28, zapište tedy číslo „1“pod číselné pole 16 a odečtěte 16 od 28, takže získáte nové číslo 12. Číslo 8 je menší než 12, napište tedy číslo „1“pod číslo 8 a odečtěte 8 od 12, abyste získali nové číslo 4.

Krok 5. Pokračujte, dokud se nedostanete na konec stolu
Pod každým políčkem nezapomeňte označit „1“pro čísla, která jsou stejná nebo menší než nové číslo, a „0“pod každým polem pro čísla, která jsou stále větší než nové číslo.
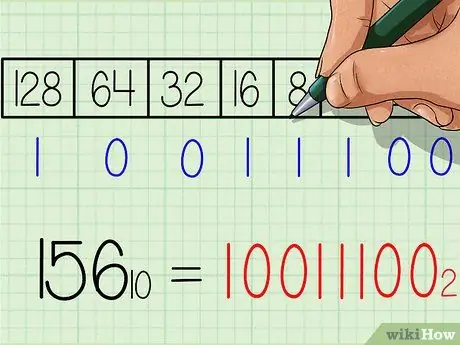
Krok 6. Zapište odpověď na binární číslo
Číslo bude přesně stejné zleva doprava jako řada čísel „1“a „0“ve spodní části tabulky. Měli byste získat výsledek 10011100. Toto je binární ekvivalent desetinného čísla 156. Nebo při zápisu s dolním indexem: 15610 = 100111002.
Opakování této metody vám může pomoci zapamatovat si síly základny dvě, takže můžete krok 1 přeskočit
Tipy
- Program Kalkulačka zabudovaný v operačním systému může tuto konverzi provést za vás, ale jako programátor je nejlepší začít s dobrým porozuměním tomu, jak převody fungují. Možnosti převodu v programu Kalkulačka lze zviditelnit otevřením nabídky „Zobrazit“a výběrem „Programátor“(pro Windows 7 a 8).
- Převod v opačném směru, tj. Z binární na desítkovou číselnou soustavu, je obvykle snazší naučit se nejprve.
- Abyste se stali odbornějšími, často cvičte převod desetinných čísel na binární.






