- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2023-12-16 11:01.
- Naposledy změněno 2025-01-23 12:14.
Existuje mnoho různých tvarů plochých tvarů a existuje mnoho důvodů, proč byste měli chtít vypočítat plochu: od domácích úkolů po odhad, kolik barvy je potřeba k překreslení obývacího pokoje. Nebojte se, wikiHow má odpověď! Začněte od kroku 1 níže, abyste věděli, jak vypočítat plochu rovinného obrázku.
Krok
Metoda 1 ze 7: Čtverec, obdélník a rovnoběžník
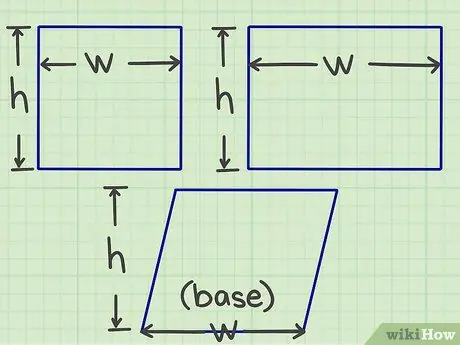
Krok 1. Změřte délku a šířku
Začněte měřit nebo zjistit délku a šířku plochého tvaru (nebo jinými slovy velikost každé ze dvou stran, které se setkávají v jednom bodě).
- Pro rovnoběžník musíte najít základnu a výšku, ale jednoduše řečeno, myšlenka je stejná jako délka a šířka.
- V reálném světě to možná budete muset změřit sami, ale pokud jde o domácí úkoly, učitel si již obvykle zapsal čísla spolu s obrázkem tvaru.
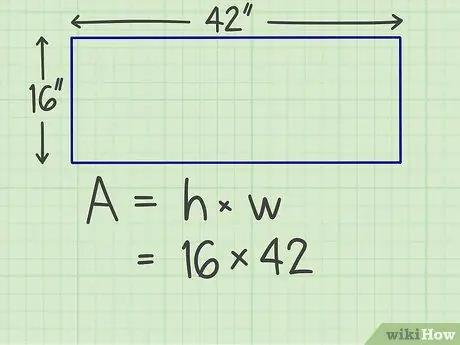
Krok 2. Vynásobte strany
Vynásobte jednu stranu druhou. Předpokládejme například, že máte obdélník o šířce 16 palců a délce 42 palců, takže musíte vypočítat 16 x 42.
Pokud počítáte plochu čtverce (dříve čtverce), ušetříte čas tím, že pomocí kalkulačky zarovnáte jednu z jeho stran. Pokud strana měří 4 m, výsledek zobrazíte stisknutím klávesy 4 a poté čtvercového tlačítka na kalkulačce. Čtverec znamená vynásobení čísla samotným
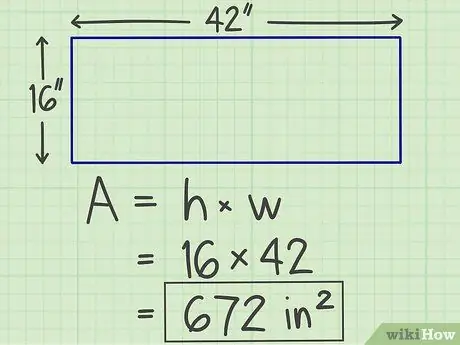
Krok 3. Zapište si výsledky
Násobení, které jste provedli dříve, vytvoří číslo, což je plocha roviny, kterou vypočítáváte, s jednotkou „čtverec“. Obdélník, který jsme vypočítali dříve, má tedy plochu 672 čtverečních palců.
Někdy je tato čtvercová jednotka také psána jako malá 2, která mírně stoupá za názvem jednotky (jako psací schopnosti)
Metoda 2 ze 7: Trapéz
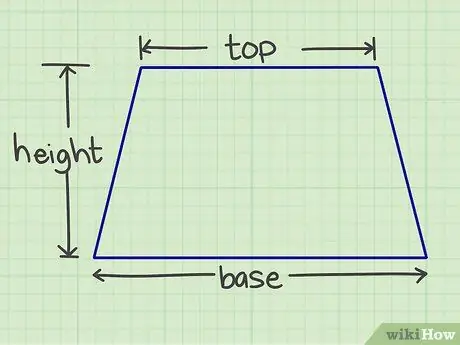
Krok 1. Změřte požadované číslo
Budete muset změřit základnu, střechu a výšku. Základna a střecha jsou rovnoběžné strany, zatímco výška je kolmá čára spojující obě rovnoběžné strany.
V reálném světě to možná budete muset změřit sami, ale pokud jde o domácí úkoly, učitel si již obvykle zapsal čísla spolu s obrázkem tvaru
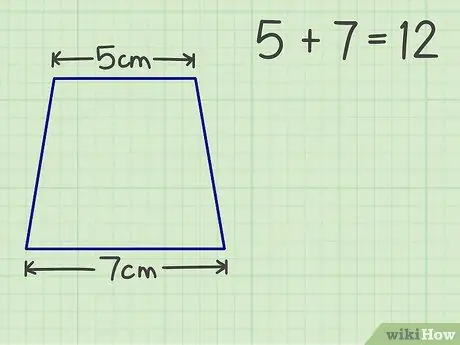
Krok 2. Sečtěte dvě rovnoběžné strany
Například náš lichoběžník má střechu 5 cm a základnu 7 cm. Součet obou rovnoběžných stran je 12.
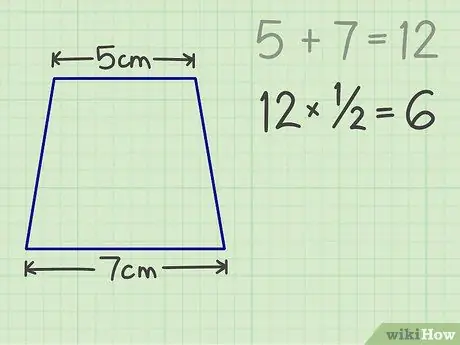
Krok 3. Vynásobte číslo 1/2, výsledkem je 6
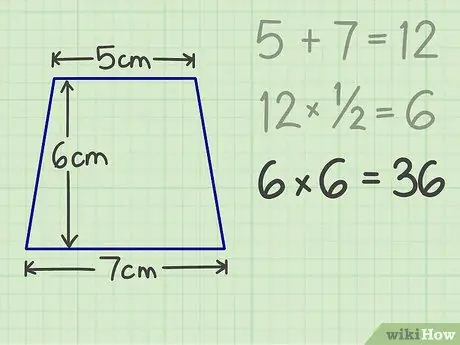
Krok 4. Poté vynásobte výsledek výškou
Pokud má lichoběžník například výšku 6 cm, konečný výsledek je 36.
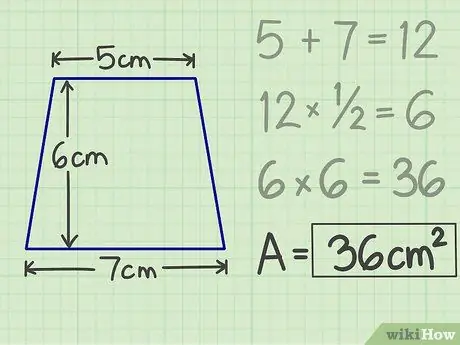
Krok 5. Zapište si výsledky
Násobení, které jste provedli dříve, vytvoří číslo, konkrétně oblast lichoběžníku. Takže pro lichoběžník se střechou 5 cm, základnou 7 cm a výškou 6 cm je plocha 36 cm čtverečních.
Metoda 3 ze 7: Kruh
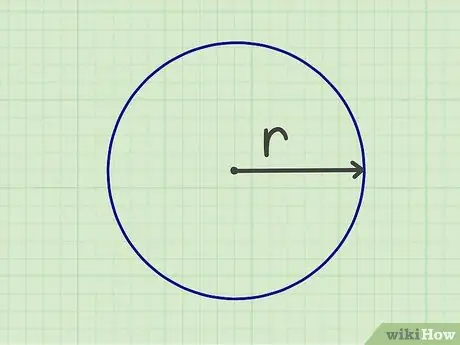
Krok 1. Změřte poloměr
Abyste mohli vypočítat plochu kruhu, musíte změřit poloměr. poloměr je vzdálenost od středu kruhu k jeho okraji. Poloměr můžete také změřit změřením průměru (šířky kruhu od okraje k okraji) a poté vydělením čísla dvěma.
V reálném světě to možná budete muset změřit sami, ale pokud jde o domácí úkoly, učitel si již obvykle zapsal čísla spolu s obrázkem tvaru
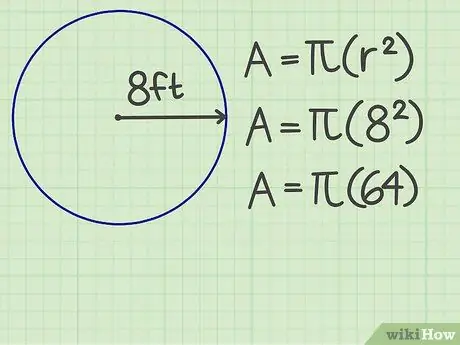
Krok 2. Zarovnejte prsty
Vynásobte počet poloměrů sám. Například poloměr kruhu je 8 stop, takže výsledkem je 64.
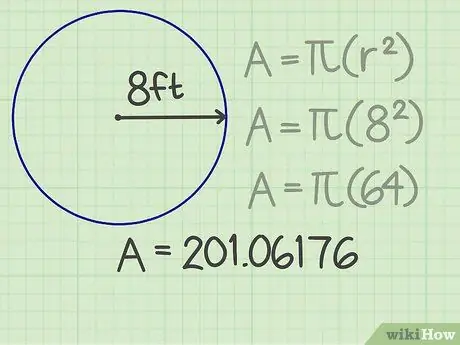
Krok 3. Výsledek vynásobte pí
Pi (π) je důležité číslo používané v různých vzorcích. Pokud používáte kalkulačku, stisknutím klávesy pi získáte skutečně přesné výsledky. Jinak pro zjednodušení výpočtů můžete za čárkou zaokrouhlit pí na několik číslic, například 3, 14159. Když toto číslo vynásobíte druhou mocninou poloměru, výsledkem je 201, 06176.
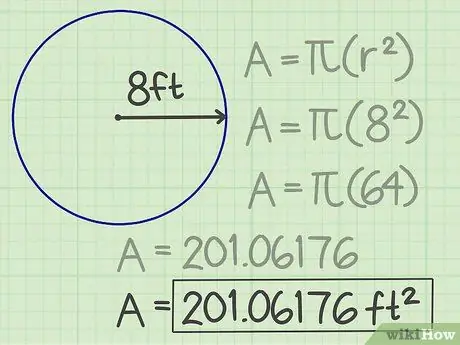
Krok 4. Zapište si výsledky
Získané číslo 201, 06176 je plocha kruhu. Jeho plocha je tedy 201 06176 čtverečních stop.
Metoda 4 ze 7: Sektor (Juring)
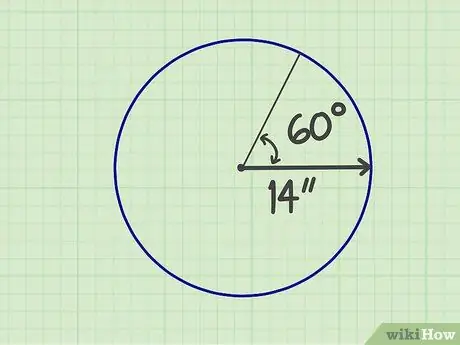
Krok 1. Změřte požadovaná čísla
Sektor je část kruhu tvořeného dvěma poloměry a hranou, takže tvar je jako vějíř. Musíte znát velikost poloměru a úhel, který tvoří „vějíř“. Předpokládejme například, že sektor má poloměr 14 palců a úhel 60 stupňů.
V reálném světě to možná budete muset změřit sami, ale pokud jde o domácí úkoly, učitel si již obvykle zapsal čísla spolu s obrázkem tvaru
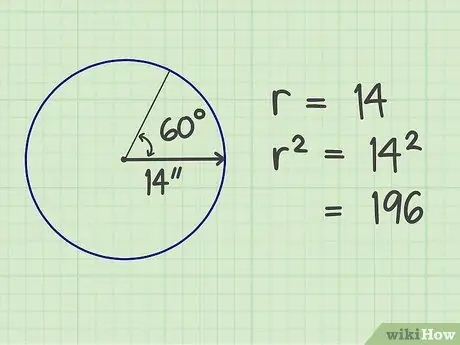
Krok 2. Zarovnejte prsty
Vynásobte počet poloměrů sám. Výsledkem je 196 (14x14).

Krok 3. Výsledek vynásobte pí
Pi (π) je důležité číslo používané v různých vzorcích. Pokud používáte kalkulačku, stisknutím klávesy pi získáte skutečně přesné výsledky. Jinak pro zjednodušení výpočtů můžete za čárkou zaokrouhlit pí na několik číslic, například 3, 14159. Pokud toto číslo vynásobíte druhou mocninou poloměru, výsledkem je 615, 75164.

Krok 4. Vydělte míru úhlu 360
Vydělte úhel sektorového ventilátoru 360 (míra úhlu plného kruhu). U výše uvedeného příkladu je výsledek kolem 0,166. Pokud jej vypočítáte pomocí kalkulačky, je výsledek ve skutečnosti delší a iterativní, ale zde je zaokrouhlen, aby byl výpočet snazší.

Krok 5. Vynásobte toto číslo předchozím číslem
Vynásobte číslo, které získáte poté, co úhel vydělíte 360, číslem, které jste získali dříve po vynásobení pí čtvercem poloměru. u výše uvedeného příkladu je výsledek 102, 214 (po zaokrouhlení).
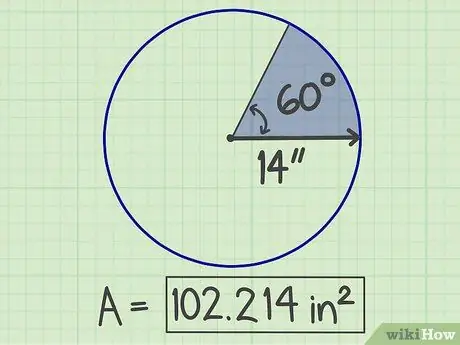
Krok 6. Zapište si výsledky
Získané číslo je plocha sektoru, která je 102 214 čtverečních palců.
Metoda 5 ze 7: Elipsa
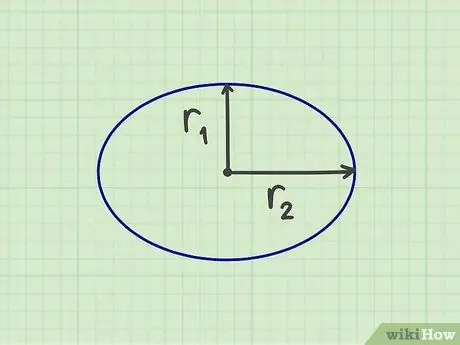
Krok 1. Změřte požadované číslo
Pro výpočet plochy elipsy je třeba změřit dva „poloměry“, a to krátký poloměr a dlouhý poloměr, což je polovina šířky a polovina výšky elipsy. Můžete také měřit krátký poloměr od středu elipsy ke nejkratší straně a dlouhý poloměr od středu elipsy k nejdelší straně. Krátký poloměr by měl tvořit pravý úhel s dlouhým poloměrem.
V reálném světě to možná budete muset změřit sami, ale pokud jde o domácí úkoly, učitel si již obvykle zapsal čísla spolu s obrázkem tvaru
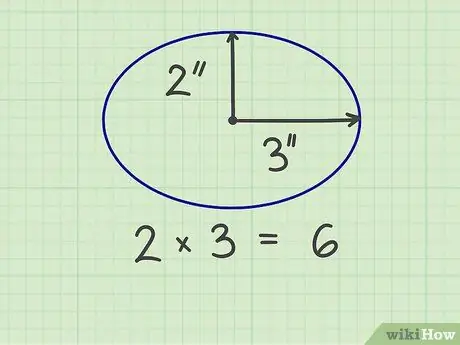
Krok 2. Vynásobte dva prsty
Například elipsa je 6 palců široká a 4 palce vysoká, takže poloměry jsou 3 palce a 2 palce. Když jsou tato dvě čísla vynásobena, výsledkem je 6 (3 x 2).

Krok 3. Výsledek vynásobte pí
Pi (π) je důležité číslo používané v různých vzorcích. Pokud používáte kalkulačku, stisknutím klávesy pi získáte skutečně přesné výsledky. V opačném případě, abyste své výpočty usnadnili, můžete za čárkou zaokrouhlit pí na několik číslic, například 3, 14159. Když toto číslo vynásobíte druhou mocninou poloměru, výsledkem je 18, 84954.
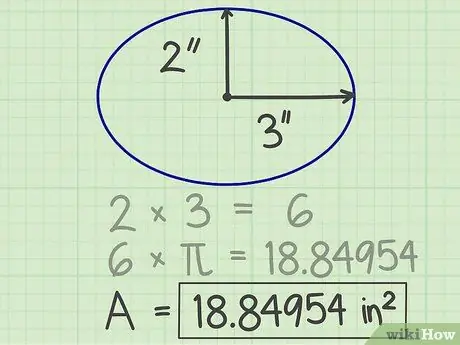
Krok 4. Zapište si výsledky
Číslo získané z výše uvedeného výpočtu je plocha elipsy. Ve výše uvedeném příkladu je plocha elipsy 18,84954 čtverečních palců.
Metoda 6 ze 7: Trojúhelník
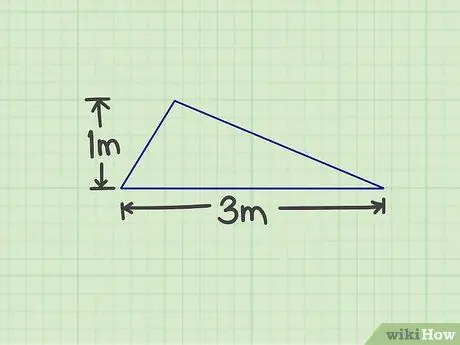
Krok 1. Změřte požadované číslo
Musíte změřit základnu a výšku trojúhelníku. Základem může být jakákoli strana trojúhelníku, pokud můžete měřit výšku. Například existuje trojúhelník se základnou 3 m a výškou 1 m.
V reálném světě to možná budete muset změřit sami, ale pokud jde o domácí úkoly, učitel si již obvykle zapsal čísla spolu s obrázkem tvaru
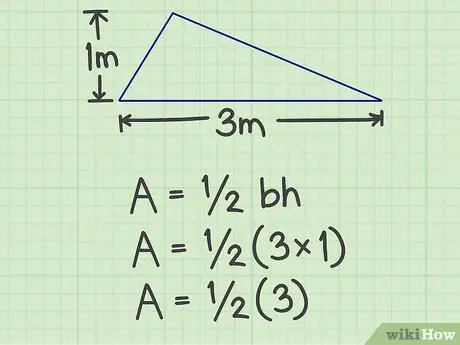
Krok 2. Vynásobte základnu výškou
U výše uvedeného příkladu je výsledek 3 (3x1).
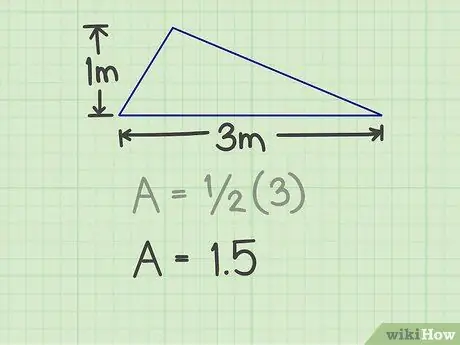
Krok 3. Výsledek vynásobte 1/2
Toto násobení vytvoří čísla 1, 5.
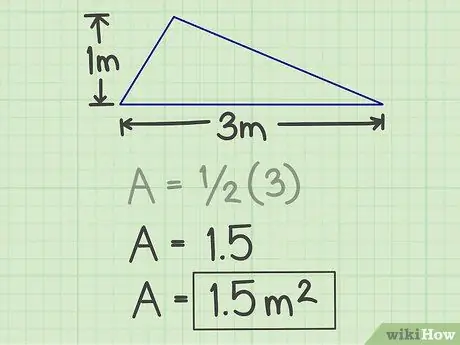
Krok 4. Zapište si výsledky
Číslo generované výše uvedeným výpočtem je plocha trojúhelníku a u výše uvedeného příkladu je jeho plocha 1,5 metru čtverečního.
Metoda 7 ze 7: Složitá plochá stavba
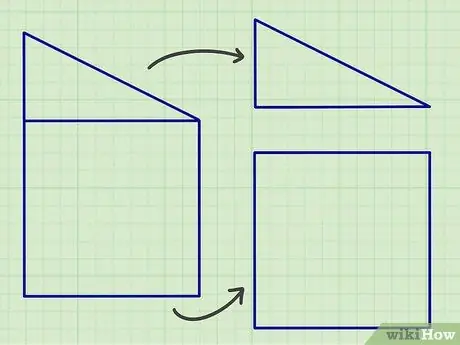
Krok 1. Rozdělte složité rovinné tvary na části sestávající ze standardních geometrických tvarů výše
Pokud to, co děláte, jsou domácí úkoly, může být snadné rozdělit složitý tvar na dříve diskutované ploché tvary, ale v reálném světě možná budete muset plochý tvar rozdělit na spoustu plochých tvarů, abyste získali přesný výsledek výpočtu..
Dobrým způsobem, jak začít, je hledat čáry, které jsou rovnoběžné nebo které tvoří určitý úhel, protože většina plochých tvarů je tvořena těmito tvary
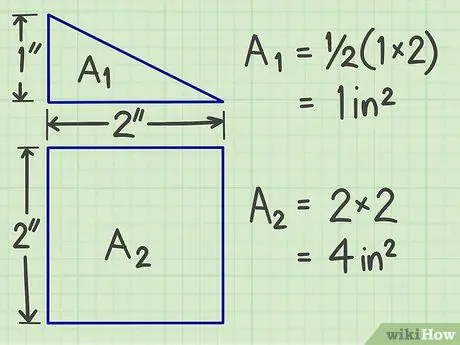
Krok 2. Vypočítejte plochu pro každý z rovinných obrazců vyplývajících z oddělení
Pomocí výše uvedených metod získáte plochu každého plochého tvaru.
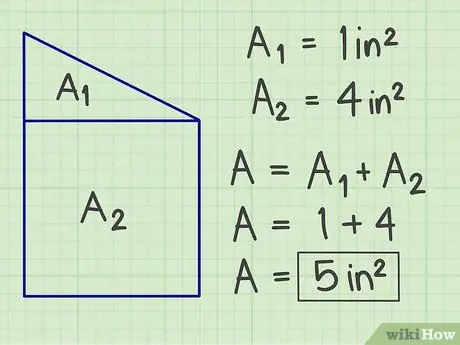
Krok 3. Sečtěte výsledky
Sečtěte všechny vypočítané oblasti, abyste získali celkovou plochu vaší komplexní rovinné figury.
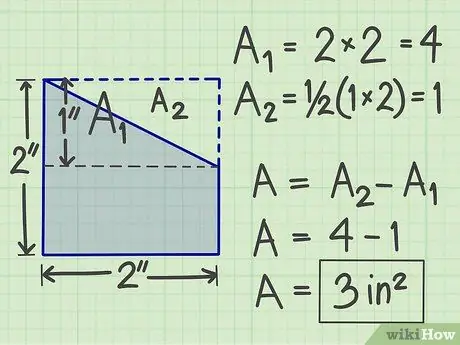
Krok 4. Použijte jinou metodu
V závislosti na tvaru složitého plochého tvaru můžete vyzkoušet mnoho dalších způsobů. Můžete k němu například také přidat imaginární rovinný tvar, aby se stal standardním geometrickým rovinným tvarem. Poté vypočítejte plochu a poté odečtěte plochu imaginárního plochého tvaru, který jste použili k přidání.
Tipy
- Tuto kalkulačku použijte, pokud potřebujete pomoc s řešením matematických výpočtů.
- Pokud máte stále potíže, požádejte o pomoc přítele!
Varování
- Vždy je lepší zkontrolovat výsledky výpočtů, abyste se ujistili, že jsou správné!
- Ujistěte se, že jednotky, které používáte, jsou při výpočtu stejné (cm, m, palce atd.), Abyste se kvůli smíšeným jednotkám nepřepočítali!






