Pomocí Spearmanova koeficientu korelační pozice můžeme identifikovat, zda mají dvě proměnné monotónní funkční vztah (to znamená, že když se jedno číslo zvýší, druhé číslo se také zvýší, nebo naopak). Chcete -li vypočítat korelační koeficient Spearmanovy hodnosti, musíte řadit a porovnávat soubory dat, abyste našli d2, a poté zadejte data do standardního nebo zjednodušeného vzorce koeficientu korelačního koeficientu Spearman. Tyto koeficienty můžete také vypočítat pomocí vzorců aplikace Excel nebo příkazu R.
Krok
Metoda 1 ze 3: Ruční způsob
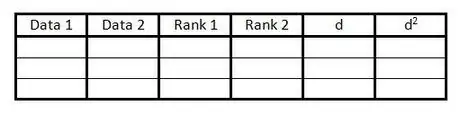
Krok 1. Vytvořte tabulku
Tabulka slouží k zahrnutí všech informací potřebných k výpočtu Spearman Rank Correlation Coefficient. Potřebujete tabulku takto:
- Vytvořte 6 sloupců s nadpisy, jako v příkladu.
- Připravte si tolik prázdných řádků, kolik je datových párů.
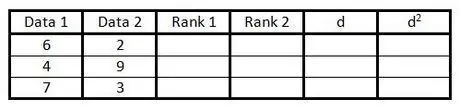
Krok 2. Vyplňte první dva sloupce datovými páry
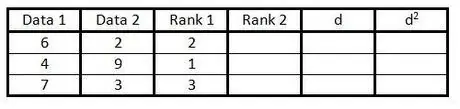
Krok 3. Zadejte pořadí prvního sloupce skupin dat ve třetím sloupci od 1 do n (počet dat)
Uveďte hodnocení 1 pro nejnižší hodnotu, hodnocení 2 pro další nejnižší hodnotu atd.
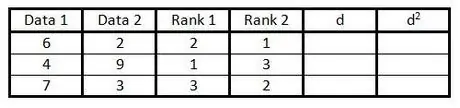
Krok 4. Ve čtvrtém sloupci proveďte totéž jako v kroku 3, ale zařaďte data do druhého sloupce
-
Průměr_742 Pokud existují dvě (nebo více) dat, která mají stejnou hodnotu, vypočítejte průměrné hodnocení dat a poté je zadejte do tabulky na základě této průměrné hodnoty.
V příkladu napravo existují dvě hodnoty 5 pro hodnocení 2 a 3. Protože existují dvě pětky, vyhledejte průměr hodnocení. Průměr 2 a 3 je 2,5, takže pro obě hodnoty 5 zadejte hodnotu hodnocení 2,5.
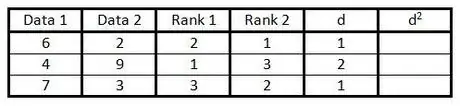
Krok 5. Ve sloupci „d“vypočítejte rozdíl mezi dvěma čísly ve sloupci pořadí
To znamená, že pokud je jeden sloupec zařazen do 1 a druhý do 3, je rozdíl 2. (Na znaménku nezáleží, protože dalším krokem je srovnat hodnotu.)
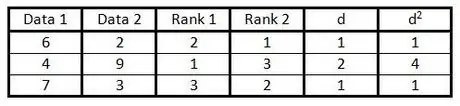
Krok 6. Srovnejte každé číslo ve sloupci „d“a výsledek napište do sloupce „d2".
Krok 7. Sečtěte všechna data ve sloupci „d2".
Výsledkem je d2.
Krok 8. Vyberte jeden z následujících vzorců:
-
Pokud žádné z hodnocení není stejné jako v předchozím kroku, zadejte tuto hodnotu do zjednodušeného vzorce Spearman Rank Correlation Coefficient
Step8_271 a nahraďte „n“počtem datových párů, abyste získali výsledek.
Krok 9_402 -
Pokud je v předchozím kroku podobná pozice, použijte standardní vzorec Spearman Rank Correlation Coefficient:
Spearman
Krok 9. Interpretujte výsledky
Hodnota se může pohybovat mezi -1 a 1.
- Pokud je hodnota blízká -1, korelace je záporná.
- Pokud je hodnota blízká 0, neexistuje lineární korelace.
- Pokud je hodnota blízká 1, je korelace kladná.
Metoda 2 ze 3: Použití aplikace Excel
Krok 1. Vytvořte nový sloupec pro data spolu s jejich hodnocením
Pokud jsou vaše data například ve sloupci A2: A11, použijte vzorec „= RANK (A2, A $ 2: A $ 11)“a zkopírujte jej, dokud nepokryje všechny sloupce a řádky.
Krok 2. Změňte stejné hodnocení, jak je popsáno v krocích 3 a 4 metody 1
Krok 3. V nové buňce vypočítejte korelaci mezi dvěma sloupci pořadí podle vzorce „= CORREL (C2: C11, D2: D11)“
V tomto případě C a D odkazují na sloupec, kde se nachází hodnocení. Nová buňka bude naplněna korelací Spearman Rank.
Metoda 3 ze 3: Použití R
Krok 1. Nainstalujte si nejprve program R, pokud jej ještě nemáte
(Viz
Krok 2. Uložte data ve formátu CSV, do prvních dvou sloupců vložte data, u kterých chcete najít korelaci
To lze provést pomocí nabídky „Uložit jako“.
Krok 3. Otevřete R Editor
Pokud pracujete z terminálu, stačí spustit R. Pokud pracujete z plochy, klikněte na ikonu R.
Krok 4. Zadejte následující příkaz:
- d <- read.csv ("NAME_OF_YOUR_CSV.csv") a stiskněte Enter.
- cast (rank (d [, 1]), rank (d [, 2]))
Tipy
Data musí sestávat alespoň z 5 párů, aby byl trend vidět (počet dat je v tomto příkladu 3 páry pouze pro zjednodušení výpočtů.)
Varování
- Korelační koeficient Spearmanovy hodnosti určuje pouze sílu korelace tam, kde data konzistentně stoupají nebo klesají. Pokud je v datech další trend, Spearmanova hodnostní korelace Ne poskytne přesné vyjádření.
- Tento vzorec je založen na předpokladu, že neexistují žádná stejná hodnocení. Pokud existuje stejná hodnost jako v příkladu, měli bychom použít tuto definici: korelační koeficient multiplikačního momentu podle hodnosti.
