- Autor Jason Gerald [email protected].
- Public 2024-02-01 14:12.
- Naposledy změněno 2025-01-23 12:14.
Vše, co potřebujete k výpočtu průměrné rychlosti, je celkový výtlak. nebo změna polohy a celkový čas. Pamatujte, že rychlost také vypočítává směr a rychlost objektu, proto do odpovědi zahrňte směr, například „sever“, „vpředu“nebo „vlevo“. Pokud váš problém s výpočtem rychlosti zahrnuje také neustálé zrychlování, můžete se naučit rychlý způsob, jak najít odpověď ještě snadněji.
Krok
Metoda 1 ze 2: Výpočet průměrné rychlosti posunu a času

Krok 1. Pamatujte, že rychlost zahrnuje jak rychlost, tak směr objektu
Rychlost popisuje rychlost, s jakou se mění poloha objektu. Souvisí to nejen s rychlostí pohybu objektu, ale také s jeho směrem. „100 metrů za sekundu na jih“je jiná hodnota rychlosti než „100 metrů za sekundu na východ“.
- Veličiny, které mají směr, se nazývají vektorové veličiny '. Toto množství lze odlišit od bezsměrného množství nazývaného skalární množství napsáním šipky nad proměnnou. Například zápis v představuje rychlost, zatímco zápis v → představuje rychlost nebo rychlost + směr. V notace použitá v tomto článku představuje rychlost.
- Ve vědeckých problémech byste měli používat metry nebo jiné metrické jednotky k vyjádření vzdálenosti, zatímco pro každodenní účely můžete použít jakoukoli jednotku, která se vám líbí.
Krok 2. Najděte celkovou hodnotu výtlaku
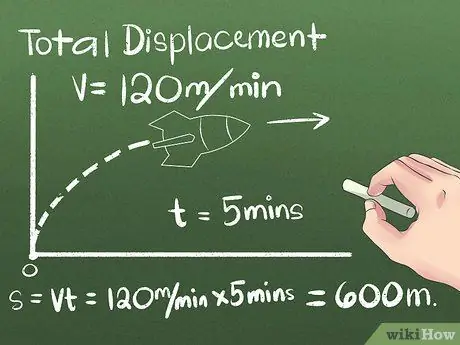
Posunutí je změna polohy objektu nebo vzdálenosti a směru mezi jeho počátečním a koncovým bodem. Směr, kterým se předmět pohybuje, než dosáhne své konečné polohy, lze zanedbat, protože se bere v úvahu pouze vzdálenost mezi počátečním a koncovým bodem. Pro první příklad použijeme předmět pohybující se konstantní rychlostí v jednom směru:
- Řekněme, že raketa se pohybuje 5 minut na sever konstantní rychlostí 120 metrů za minutu. Chcete -li vypočítat konečnou polohu, použijte vzorec s = vt, nebo pomocí praktického myšlení vypočítejte vzdálenost, kterou raketa poté urazí (5 minut) (120 metrů/minutu) = 600 metrů severně z výchozího bodu.
- U problémů zahrnujících konstantní zrychlení je můžete vyřešit pomocí s = vt + at2, nebo použijte krátkou metodu popsanou v jiné části, abyste našli odpověď.
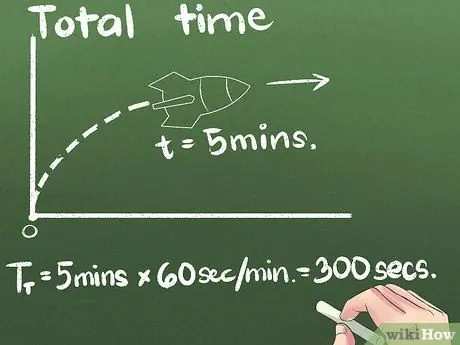
Krok 3. Najděte celkový strávený čas
V našem příkladu se raketa pohybuje dopředu o 5 minut. Průměrnou rychlost můžete vyjádřit v jakékoli časové jednotce, ale druhá je mezinárodní vědecká standardní jednotka. V tomto případě změníme jednotky sekund: (5 minut) x (60 sekund/minuta) = 300 sekund.
I ve vědeckých problémech, pokud otázka používá hodinu nebo větší jednotku času, bude jednodušší nejprve vypočítat rychlost a poté převést konečnou odpověď na metry/sekundu
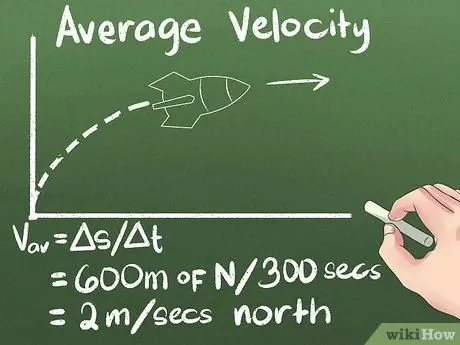
Krok 4. Vypočítejte průměrnou rychlost jako výtlak v čase
Pokud víte, jak daleko se předmět pohybuje, a jak dlouho bude trvat, než se tam dostanete, budete vědět, jak rychle se pohybuje. Pro příklad, který používáme, je průměrná rychlost rakety (600 metrů severně) / (300 sekund) = 2 metry za sekundu na sever.
- Nezapomeňte uvést směr (například „vpředu“nebo „sever“).
- Ve vzorci protiav = s/Δt. Symbol delta znamená „změna“, takže s/Δt znamená „změna polohy za určité časové období“.
- Průměrnou rychlost lze zapsat jako vav, nebo jako v s vodorovnou čarou nad ním.

Krok 5. Vyřešte složitější problémy
Pokud předmět změní svůj směr nebo rychlost, nenechte se zmást. Průměrná rychlost je stále „pouze“počítána z celkového výtlaku a celkového času. Co se stane mezi počátečním a koncovým bodem, můžete ignorovat. Následuje několik příkladů pohybu objektu se stejným výtlakem a celkovým časem, a tedy stejnou průměrnou rychlostí:
-
Anna kráčí 2 sekundy na západ rychlostí 1 metr/s, pak náhle zrychlí na 3 metry/sekundu a pokračuje v chůzi na západ po dobu 2 sekund. Celkový výtlak je (1 m/s na západ) (2 s) + (3 m/s na západ) (2 s) = 8 metrů na západ. Celkový čas je 2 sekundy + 2 sekundy = 4 sekundy. Průměrná rychlost je tedy 8 metrů na západ/ 4 sekundy = 2 metry za sekundu na západ.
- Bart kráčí 3 sekundy na západ rychlostí 5 metrů/s, pak se otočí a 1 sekundu kráčí na východ rychlostí 7 metrů/s. Pohyb na východ můžeme považovat za „negativní pohyb na západ“, takže celkový výtlak je = (5 metrů/s na západ) (3 s) + (-7 m/s na západ) (1 s) = 8 metrů. Celkový čas = 4 sekundy. Průměrná rychlost = 8 metrů na západ / 4 sekundy = 2 metry za sekundu na západ.
-
Charlotte šla na sever 1 metr a pak šla na západ 8 metrů, pak na jih 1 metr. Čas potřebný k dokončení celé cesty jsou 4 sekundy. Nakreslete diagram na kousek papíru a uvidíte, že koncový bod je 8 metrů západně od počátečního bodu, takže tato hodnota je posunutí. Celkový čas je 4 sekundy, průměrná rychlost je tedy 8 metrů na západ / 4 sekundy = 2 metry za sekundu na západ.
Metoda 2 ze 2: Výpočet průměrné rychlosti fixního zrychlení

Krok 1. Zvažte počáteční rychlost a konstantní zrychlení
Řekněme, že náš problém je „Jízdní kolo se pohybuje doprava rychlostí 5 m/s, s konstantním zrychlením 2 m/s2. Pokud se toto kolo pohybuje po dobu 5 sekund, jaká je jeho průměrná rychlost?"
Pokud jednotka "metr/s2„aby vás to zmátlo, napište to jako„ metry/sekundu/sekundu “nebo„ metry za sekundu za sekundu. “Zrychlení 2 metry za sekundu/sekundu znamená, že rychlost se zvyšuje o 2 metry za sekundu každou sekundu.

Krok 2. Použijte zrychlení k nalezení konečné rychlosti
Zrychlení, označované notací a, je rychlost změny rychlosti (nebo rychlosti). Rychlost se zvyšuje konstantní rychlostí růstu. Pomocí zrychlení můžete nakreslit tabulku a zjistit tak rychlost v různých časech během jízdy na kole. Tuto tabulku musíme vytvořit, abychom našli koncový bod problému (v čase t = 5 sekund), ale vytvoříme delší tabulku, která vám usnadní pochopení tohoto konceptu:
- Ve výchozím bodě (čas t = 0 sekund) se kolo pohybuje rychlostí 5 metrů/s.
- Po 1 sekundě (t = 1) se kolo pohybuje rychlostí 5 metrů/sekundu + rychlostí = 5 metrů/sekundu + (2 metry/sekundu2) (1 sekunda) = 7 metrů za sekundu.
- Při t = 2 se kolo pohybuje doprava rychlostí 5+ (2) (2) = 9 metrů/s.
- Při t = 3 se kolo pohybuje doprava rychlostí 5+ (2) (3) = 11 metrů/s.
- Při t = 4 se kolo pohybuje doprava rychlostí 5+ (2) (4) = 13 metrů/s.
- Při t = 5 se kolo pohybuje doprava rychlostí 5+ (2) (5) = 15 metrů za sekundu.

Krok 3. Pomocí tohoto vzorce zjistíte průměrnou rychlost
Pokud a „pouze“, pokud je zrychlení konstantní, bude průměrná rychlost rovna průměrné hodnotě součtu konečných a počátečních rychlostí. (protiF +vjá)/2. Pro náš výše uvedený příklad je počáteční rychlost kola vjá 5 metrů za sekundu. Poté, co vypočítáme, je konečná rychlost vF 15 metrů za sekundu. Sečtením těchto dvou hodnot dohromady dostaneme (15 metrů/sekundu + 5 metrů/sekundu)/2 = (20 metrů/sekundu)/2 = 10 metrů za sekundu správným směrem.
- Nezapomeňte uvést směr, v tomto případě „správný“.
- Tento výraz lze zapsat jako v0 (rychlost v čase 0 nebo počáteční rychlost) a v (konečná rychlost).

Krok 4. Pochopte vzorec průměrné rychlosti intuitivně
Abychom našli průměrnou rychlost, můžeme použít rychlost v kterémkoli bodě a najít průměr pro všechny z nich. (Toto je definice průměru.) Protože to vyžaduje kalkul nebo nekonečný čas, rozumějte tomuto vzorci intuitivněji. Místo toho, abyste pokaždé brali, vypočítejte průměrnou rychlost dvou časových bodů a podívejte se na výsledky. Jeden časový okamžik je blízko začátku jízdy, kdy kolo jede pomalu, a další bod je blízko koncového bodu, kde kolo jede rychle.

Krok 5. Otestujte intuitivní teorii
Pomocí výše uvedené tabulky určete rychlost v různých časových bodech. Některé páry, které splňují naše kritéria, jsou (t = 0, t = 5), (t = 1, t = 4) nebo (t = 2, t = 3). Pokud chcete, můžete tento vzorec otestovat také s jinými hodnotami než celými čísly.
Ať už si vyberete jakýkoli pár bodů, průměrná rychlost v té době bude vždy stejná. Například (((5+15)/2), ((7+13)/2), nebo ((9+11)/2) all right 10 metres/sec to right

Krok 6. Dokončete intuitivní vysvětlení
Použijeme -li tuto metodu se seznamem všech časů, budeme pokračovat ve výpočtu průměru první poloviny cesty a druhé poloviny cesty. Čas potřebný k pokrytí každé poloviny je stejný, takže po dokončení počítání se neztratí žádná rychlost.
- Protože každý pár poskytne stejný výsledek, průměr těchto rychlostí bude také stejný v hodnotě. V našem případě je rychlost celku „10 metrů/s doprava“stále 10 metrů/s vpravo.
- Tuto hodnotu můžeme zjistit výpočtem průměru jakéhokoli páru, například počáteční a konečné rychlosti. V našem případě jsou tyto rychlosti dosaženy při t = 0 a t = 5 a lze je vypočítat pomocí výše uvedeného vzorce: (5+15)/2 = 10 metrů/s vpravo.

Krok 7. Pochopte tento vzorec matematicky
Pokud vám více vyhovují důkazy zapsané jako vzorce, můžete začít se vzorcem pro výpočet ujeté vzdálenosti za předpokladu konstantního zrychlení a odtud odvodit vzorec:
- s = vját + v2. (Technicky s a t, nebo změna polohy a změna v čase, ale pochopili byste také, kdybyste napsali s a t.)
- Průměrná rychlost vav definováno jako s/t, zadejte tedy vzorec ve tvaru s/t.
- protiav = s/t = vjá + v
- Zrychlení x čas se rovná změně celkové rychlosti nebo vF - vjá. Ve vzorci tedy můžeme nahradit „at“a získat:
- protiav = vjá + (vF - vjá).
- Zjednodušit: vav = vjá + vF - vjá = vjá + vF = (protiF +vjá)/2.
Tipy
- Rychlost se liší od rychlosti, protože rychlost je vektorová veličina, zatímco rychlost je skalární veličina. Vektorové veličiny zahrnují jak směr, tak velikost, zatímco skalární veličiny zahrnují pouze velikost.
- Pokud se objekt pohybuje v jedné dimenzi, například zleva doprava, můžete použít kladné číslo k reprezentaci jednoho směru (například doprava) a záporné číslo k označení jiného směru (vlevo). Napište tento zápis do horní části stránky, aby byl srozumitelný lidem, kteří čtou vaši práci.






