- Autor Jason Gerald [email protected].
- Public 2024-01-16 19:16.
- Naposledy změněno 2025-01-23 12:14.
Rychlost je výpočet toho, jak rychle se něco pohybuje najednou. Pokud jste se někdy podívali na rychloměr jedoucího auta, uvidíte počet rychlostí - čím dále jehla jede, tím vyšší je rychlost vozidla. V závislosti na typu informací, které máte, existuje několik způsobů, jak vypočítat rychlost. Obecně vzorec rychlost = vzdálenost/čas (nebo k = j/w) je nejjednodušší způsob výpočtu rychlosti.
Krok
Metoda 1 ze 3: Použití vzorců pro výpočet standardní rychlosti

Krok 1. Najděte vzdálenost, kterou předmět urazil
Základní vzorec, který většina lidí používá k nalezení rychlosti něčeho, je velmi snadno použitelný. Nejprve musíte vědět, „jak velkou vzdálenost měřený objekt urazil“. Jinými slovy, jaká je vzdálenost mezi počátečním bodem a koncovým bodem objektu?
Tento vzorec je snáze pochopitelný na příkladu. Řekněme, že cestujeme autem na hřiště „161 kilometrů“. V několika krocích můžeme tyto informace použít k dokončení výpočtu vzorce

Krok 2. Najděte čas, za který objekt danou vzdálenost urazí
Další informace, kterou potřebujete, je, jak dlouho trvá objektu dosáhnout určité vzdálenosti. Jinými slovy, jak dlouho trvá, než se objekt přesune z počátečního bodu do koncového bodu?
V tomto případě řekněme, že objekt zabere cca. dvě hodiny dostat se do cíle.

Krok 3. Vydělte vzdálenost časem potřebným k nalezení rychlosti objektu
K tomu, abyste znali rychlost objektu, potřebujete pouze tyto dvě informace. Vzdálenost času se rovná rychlosti objektu.
V tomto případě 161 kilometrů/2 hodiny = 80,5 kilometru za hodinu.

Krok 4. Nezapomeňte na použitou jednotku
Ve své odpovědi je velmi důležité použít správné jednotky (například kilometry za hodinu atd.) Bez těchto jednotek je pro lidi velmi obtížné pochopit význam vaší odpovědi. Body můžete také ztratit, pokud při plnění úkolů ze školy použijete špatnou jednotku.
Jednotka rychlosti je jednotka vzdálenosti k jednotce času. Protože například měříme vzdálenost v kilometrech a čas v hodinách, použité jednotky jsou kilometry/hod (nebo kilometry za hodinu).
Metoda 2 ze 3: Řešení obtížnějších výpočtů

Krok 1. Najděte několik různých proměnných k vyřešení problému vzdálenosti a času
Jakmile porozumíte základnímu vzorci rychlosti, můžete jej použít k provádění jiných výpočtů než rychlosti. Pokud například zpočátku znáte pouze rychlost objektu a jednu další proměnnou, můžete přeskupit vzorec výše, abyste našli neznámé informace.
-
Řekněme například, že víme, že vlak jede rychlostí 20 kilometrů za hodinu čtyři hodiny, ale nevíme, jak daleko urazil. Abychom to zjistili, můžeme vzorec přeskupit následujícím způsobem:
-
- rychlost = vzdálenost/čas
- rychlost × čas = (vzdálenost/čas) × čas
- rychlost × čas = vzdálenost
- 20 km/hod × 4 hodiny = vzdálenost = 80 kilometrů
-

Krok 2. Převeďte podle potřeby jednotky, které používáte
Někdy můžete rychlost vypočítat pomocí určité jednotky, ale musíte ji převést na jinou jednotku. V takovém případě musíte použít převodní faktor, abyste získali odpověď podle správných jednotek. Chcete -li to provést, jednoduše napište vztah mezi jednotkami ve zlomkové formě a znásobte. Při násobení obraťte zlomek podle potřeby, abyste odstranili nežádoucí jednotky. Tato metoda je mnohem jednodušší, než se zdá!
-
Řekněme například, že ve výše uvedeném příkladovém problému potřebujeme odpověď v kilometrech místo v kilometrech. Jedna míle se rovná asi 1,6 kilometru. Převod tedy můžeme provést následovně:
-
- 80 kilometrů × 1 míle/1,6 kilometru = 50 mil
-
- Pamatujte, že protože kilometry se objevují na konci zlomku, odstraní to kilometry z předchozí odpovědi, takže konečný výsledek používá míle.
- Tento web poskytuje funkce převodu pro většinu běžně používaných jednotek.

Krok 3. Podle potřeby nahraďte proměnnou „vzdálenost“vzorcem vzdálenosti
Objekty se nepohybují vždy po rovné, hladké dráze. Pokud je to pravda, možná nebudete moci jednoduše zadat číselnou hodnotu jako jednotku vzdálenosti do vzorce standardní rychlosti. Možná však budete muset nahradit písmeno j ve vzorci k = j/w vzorcem, který se podobá vzdálenosti uražené objektem.
-
Řekněme například, že se letadlo otáčí vzduchem na vzdálenost 20 mil 5krát. Letadlo dokončilo kolo za půl hodiny. V tomto příkladu ještě potřebujeme zjistit celkovou vzdálenost, kterou letadlo urazilo, než můžeme určit jeho rychlost. V tomto vzorci můžeme místo j použít vzorec pro výpočet vzdálenosti kolem kruhu (vzdálenost kolem něj). Tento vzorec je obvod = 2πr, kde r = poloměr kruhu. Zde je postup, jak to vyřešit:
-
- k = (2 × × r)/š
- k = (2 × × 10)/0,5
- k = 62,83/0,5 = 125,66 mil za hodinu
-

Krok 4. Pochopte, že k = j/w udává průměrnou rychlost
Snadný a jednoduchý vzorec, který používáme k nalezení rychlosti, má jednu nevýhodu. Výsledná hodnota je technicky průměrná rychlost. To znamená, že vzorec předpokládá, že měřený objekt používá stejnou rychlost, jakou se pohybuje. Jak uvidíme níže, nalezení rychlosti objektu v jediném okamžiku bude mnohem obtížnější.
Pro ilustraci tohoto rozdílu si představte, kdy jste naposledy cestovali autem. Je nepravděpodobné, že budete cestovat stejnou rychlostí, jakou cestujete. Cestu však obvykle zahájíte nízkou rychlostí a po cestě postupně zvyšujete rychlost, zastavujete kvůli červeným světelům, zácpám atd. Pokud k určení rychlosti během jízdy použijete standardní vzorec rychlosti, změny této rychlosti nelze detekovat. Dostanete však odpověď, která ukazuje průměrnou rychlost všech rychlostních rozdílů, kterými cestujete
Metoda 3 ze 3: Výpočet okamžité rychlosti
Poznámka:
Tato část používá techniky, které jsou méně známé lidem, kteří nikdy nestudovali kalkul. Přečtěte si naše články o kalkulu o pomoc.
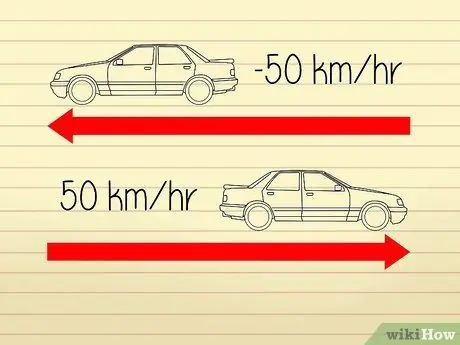
Krok 1. Pochopte, že rychlost je definována jako rychlost zrychlení
Výpočty rychlosti na vysoké úrovni jsou docela matoucí, protože matematici a vědci používají různé definice k popisu „rychlosti“a „zrychlení“. Zrychlení má dvě složky: „rychlost“a „směr“. Rychlost se rovná rychlosti objektu. Změna směru způsobí změnu zrychlení, nikoli však změnu rychlosti.
- Řekněme například, že se dvě auta pohybují v opačných směrech. Rychloměry na obou autech ukazují číslo 50 km/h, takže oba jedou stejnou rychlostí. Protože se však auta od sebe vzdalují, můžeme říci, že jedno z vozů má „zrychlení“-50 km/h, zatímco druhé má „zrychlení“50 km/h.
- Stejně jako výpočty okamžité rychlosti můžete také provádět výpočty okamžité akcelerace.

Krok 2. K měření záporného zrychlení použijte absolutní hodnoty
Objekt může mít negativní rychlost zrychlení (pokud se pohybuje v negativním směru vzhledem k jinému objektu). Negativní rychlost však neexistuje. V tomto případě tedy absolutní hodnota rychlosti udává rychlost objektu.
Z tohoto důvodu ve výše uvedeném příkladu mají oba vozy rychlost 50 km/h.
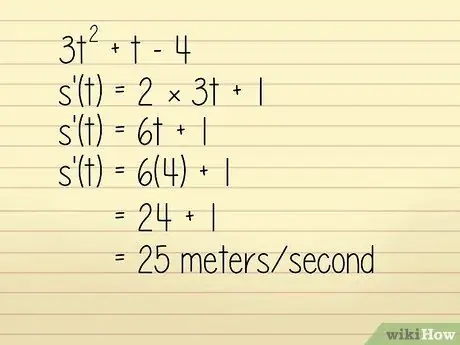
Krok 3. Vezměte derivaci polohy funkce
Pokud máte funkci k (w), která ukazuje polohu objektu, aniž byste museli počítat čas, derivace k (w) ukáže zrychlení bez potřeby časování. Stačí do tohoto vzorce zapojit hodnotu času, aby se proměnná w (nebo jakákoli hodnota času použije) zrychlila podle toho času. Odtud můžete snadno zjistit rychlost objektu.
-
Řekněme například, že poloha objektu v jednom metru je popsána v rovnici 3q2 + w - 4 kde w = čas v sekundách. Chceme znát rychlost objektu při w = 4 sekundy. V takovém případě to můžete vyřešit takto:
-
- 3w2 +w - 4
- k '(w) = 2 × 3w + 1
- k '(w) = 6w + 1
-
-
Nyní zadáme w = 4:
-
- k '(w) = 6 (4) + 1 = 24 + 1 = 25 metrů za sekundu. Technicky se jedná o výpočet zrychlení, ale protože je kladný a směr není v otázce uveden, můžeme jej použít k nalezení rychlosti.
-

Krok 4. Vezměte integrovanou funkci zrychlení
Zrychlení je způsob měření změny zrychlení objektu v čase. Toto téma je příliš složité na to, aby bylo možné ho v tomto článku plně vysvětlit. Je však užitečné poznamenat, že když máte funkci a (w), která představuje zrychlení s ohledem na čas, integrál a (w) vrátí výsledek zrychlení na základě tohoto času. Pamatujte, že je velmi užitečné znát počáteční zrychlení objektu, abyste mohli definovat konstantu tohoto výsledku z nekonečného integrálu.
-
Řekněme například, že objekt má konstantní zrychlení (v m/s2 v důsledku a (w) = -30. Také řekněte, že objekt má počáteční zrychlení 10 m/s. Potřebujeme najít rychlost w = 12 sekund. V tomto případě to můžeme vyřešit takto:
-
- a (w) = -30
- p (w) = a (w) dw = -30dw = -30w + C
-
-
Abychom našli C, budeme řešit p (w) pro w = 0. Pamatujte, že počáteční zrychlení objektu je 10 m/s.
-
- p (0) = 10 = -30 (0) + C
- 10 = C, takže p (w) = -30w + 10
-
-
Nyní můžeme zadat w = 12 sekund.
-
- p (12) = -30 (12) + 10 = -360 + 10 = -350. Protože rychlost je absolutní hodnota zrychlení, rychlost objektu je 350 metrů za sekundu.
-
Tipy
- Cvičení je skvělé! Pokuste se vytvořit vlastní otázku nahrazením čísel ve výše uvedeném příkladu.
- Pokud hledáte rychlý způsob procvičování počtu pro lepší rychlost výpočtu, použijte online derivační kalkulačku zde a online integrovanou kalkulačku zde.






