- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-16 19:16.
- Naposledy změněno 2025-01-23 12:14.
Při studiu optických přístrojů je „zvětšení“objektivu podobného objektivu poměr výšky obrazu, který vidíte, ke skutečné výšce objektu. Například čočka, díky které může objekt vypadat velmi velký, má „vysoký“faktor zvětšení, zatímco objektiv, díky němuž předmět vypadá malý, má „nízký“faktor zvětšení. Vzorec pro zvětšení objektu se obvykle vypočítá pomocí vzorce M = (vjá/hÓ) = -(djá/dÓ), kde M = zvětšení, hjá = výška obrázku, hÓ = výška objektu adjá a DÓ = vzdálenost obrazu a objektu.
Krok
Metoda 1 ze 2: Výpočet zvětšení jednoho objektivu
Poznámky: A. konvergující objektiv ve středu širší než na okrajích (jako lupa). A divergentní čočka na okrajích širší než ve středu (jako mísa). Výpočet zvětšení na obou čočkách je stejný, s jedna důležitá výjimka. Kliknutím sem přejdete přímo na výjimky u odlišných čoček.
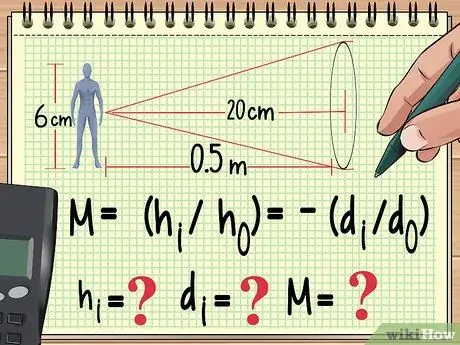
Krok 1. Začněte svou rovnicí a proměnnými, které již znáte
Stejně jako jakýkoli jiný problém z fyziky, způsob, jak vyřešit problém rozšíření, je zapsat si rovnici, kterou použijete pro jeho výpočet. Odtud můžete pracovat zpět a najít hodnotu proměnné, kterou jste nenašli z rovnice, kterou používáte.
-
Předpokládejme například, že 6 cm vysoká panenka je umístěna jeden metr od a konvergující objektiv s ohniskovou vzdáleností 20 cm. Pokud chceme vypočítat zvětšení, výšku obrázku a vzdálenost obrazu, můžeme začít psát naši rovnici následovně:
-
- M = (vjá/hÓ) = -(djá/dÓ)
-
- Nyní víme hÓ (výška panenky) a dÓ (vzdálenost panenky od objektivu). Známe také ohniskovou vzdálenost objektivu, která v této rovnici není. Budeme počítat hjádjáa M.

Krok 2. Použití rovnice čočky k získání djá.
Pokud znáte vzdálenost od zvětšovaného objektu a ohniskovou vzdálenost objektivu, je výpočet vzdálenosti od vytvořeného obrazu pomocí rovnice objektivu velmi snadný. Rovnice čočky je 1/f = 1/dÓ + 1/djá, kde f = ohnisková vzdálenost čočky.
-
V tomto příkladu problému můžeme použít rovnici čočky k výpočtu djá. Zadejte hodnoty f a djá pak vyřešte rovnici:
-
- 1/f = 1/dÓ + 1/djá
- 1/20 = 1/50 + 1/djá
- 5/100 - 2/100 = 1/djá
- 3/100 = 1/djá
- 100/3 = djá = 33,3 cm
-
- Ohnisková vzdálenost čočky je vzdálenost od středu čočky k bodu, kde je světlo v ohnisku přenášeno. Pokud jste někdy zaměřili světlo pomocí lupy na hořící mravence, viděli jste to. V otázkách v lekci byla obvykle uvedena velikost tohoto hotspotu. V reálném životě jsou tyto specifikace obvykle napsány na štítku umístěném na objektivu.

Krok 3. Výpočet hjá.
Poté, co vypočítáte dÓ a Djá, můžete vypočítat výšku zvětšeného objektu a zvětšení objektivu. Všimněte si dvou rovných znaků v rovnici zvětšení čočky (M = (hjá/hÓ) = -(djá/dÓ)) - to znamená, že všechny části této rovnice jsou si navzájem stejné, takže můžeme vypočítat M a hjá v jakémkoli pořadí chceme.
-
Pro tento příklad problému můžeme vypočítat hjá takhle:
-
- (hjá/hÓ) = -(djá/dÓ)
- (hjá/6) = -(33, 3/50)
- hjá = -(33, 3/50) x 6
- hjá = - 3 996 cm
-
- Všimněte si, že výška objektu je zde záporná, což naznačuje, že obrázek, který uvidíme později, bude převrácen (shora dolů).

Krok 4. Výpočet M
Poslední proměnnou můžete vypočítat pomocí rovnice -(djá/dÓ) nebo (hjá/hÓ).
-
V následujícím příkladu je výpočet M následující:
-
- M = (vjá/hÓ)
- M = (-3, 996/6) = - 0, 666
-
-
Výsledek bude také stejný při výpočtu pomocí hodnoty d:
-
- M = -(djá/dÓ)
- M = -(33, 3/50) = - 0, 666
-
- Mějte na paměti, že zoom nemá označení jednotky.
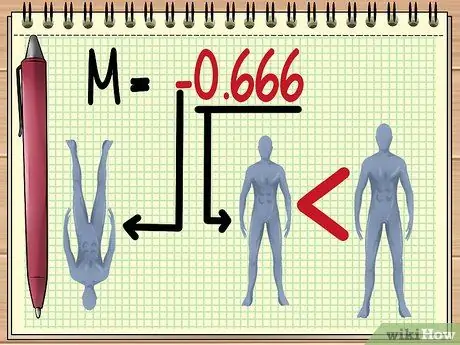
Krok 5. Pochopení hodnoty M
Jakmile získáte velikost hodnoty M, můžete odhadnout několik věcí o obrazu, který uvidíte objektivem, a to:
-
Velikost.
Čím větší je „absolutní hodnota“M, tím větší bude objekt zobrazený objektivem. Hodnota M mezi 0 až 1 znamená, že objekt bude vypadat menší.
-
Orientace objektu.
Záporná hodnota znamená, že vytvořený obraz bude obrácen.
- V uvedeném příkladu hodnota M -0,666 znamená, že podle hodnoty stávající proměnné bude viditelný stín panenky. vzhůru nohama a o dvě třetiny menší než skutečná velikost.
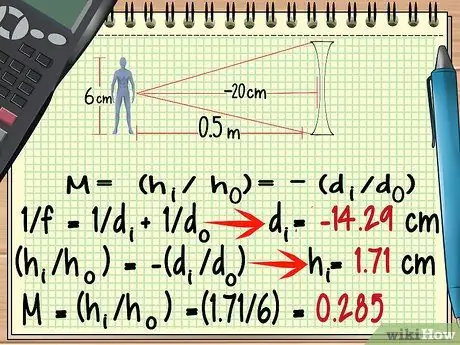
Krok 6. U rozbíhajících se čoček použijte negativní ohnisko
Přestože se tvar rozbíhající se čočky velmi liší od čočky konvergující, můžete její zvětšení vypočítat pomocí stejného vzorce jako výše. Výjimky, které je třeba mít na paměti, jsou Ohnisko rozbíhající se čočky je záporné.
Ve výše uvedeném příkladu to ovlivní odpověď, kterou získáte při výpočtu djá, takže tomu věnujte pozornost.
-
Přepracujme příkladový problém výše, teprve nyní použijeme rozbíhající se objektiv s ohniskovou vzdáleností - 20 cm.
Ostatní proměnné zůstávají na stejné hodnotě.
-
Nejprve vypočítáme djá pomocí rovnice čočky:
-
- 1/f = 1/dÓ + 1/djá
- 1/-20 = 1/50 + 1/djá
- -5/100 - 2/100 = 1/djá
- -7/100 = 1/djá
- -100/7 = djá = - 14, 29 cm
-
-
Nyní vypočítáme hjá a M s hodnotou djá nový.
-
- (hjá/hÓ) = -(djá/dÓ)
- (hjá/6) = -(-14, 29/50)
- hjá = -(-14, 29/50) x 6
- hjá = 1,71 cm
- M = (vjá/hÓ)
- M = (1, 71/6) = 0, 285
-
Metoda 2 ze 2: Výpočet zvětšení více čoček
Jednoduchá metoda se dvěma objektivy
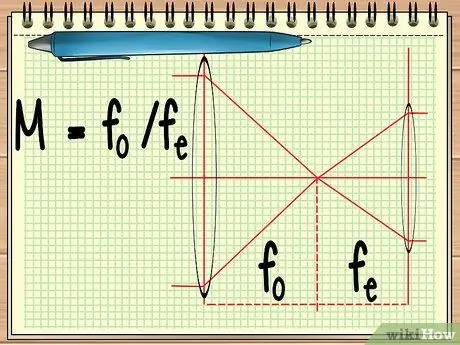
Krok 1. Vypočítejte ohnisko obou čoček
Když použijete nástroj, který se skládá ze dvou čoček uspořádaných vedle sebe (například dalekohled nebo dalekohled), stačí pro výpočet celkového zvětšení obou čoček zjistit ohnisko obou čoček. to lze vypočítat jednoduchou rovnicí M = fÓ/FE.
V rovnici fÓ je ohniskem objektivu a fE je ústředním bodem okuláru. Objektiv je velká čočka, která je blízko objektu, zatímco oční čočka je čočka, která se nachází blízko oka pozorovatele.

Krok 2. Zapojte informace, které již máte, do rovnice M = fÓ/FE.
Jakmile máte ohniska obou čoček, je velmi snadné je vypočítat, - vypočítejte poměr vydělením ohniskové vzdálenosti čočky objektivu ohniskovou vzdáleností okuláru. Odpověď, kterou dostanete, je celkové zvětšení nástroje.
-
Předpokládejme například jednoduchý dalekohled, píše se, že ohniskový bod objektivu je 10 cm a ohniskový bod okuláru je 5 cm, pak je zvětšení 10/5 = 2.
Složitá metoda
Krok 1. Vypočítejte vzdálenost mezi čočkami a předmětem
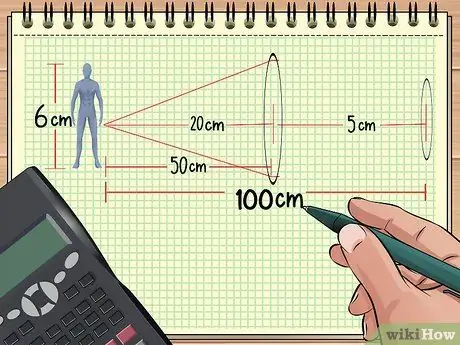
Pokud máte dva objektivy uspořádané v řadě před objektem, lze celkové zvětšení vypočítat, pokud znáte vzdálenost od objektivů k objektu, velikost objektu a ohnisko obou čoček. Lze vypočítat i zbytek.
Předpokládejme například, že uspořádáme předměty a čočky jako v příkladu problému 1 výše: panenka je 50 cm od sbíhavého objektivu, který má ohniskovou vzdálenost 20 cm. Nyní umístěte druhý objektiv s ohniskovým bodem 5 cm ve vzdálenosti 50 cm od prvního objektivu (100 cm od panenky.) Poté vypočítáme celkové zvětšení pomocí informací, které jsme získali
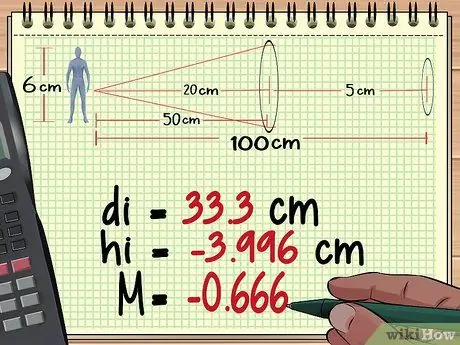
Krok 2. Vypočítejte vzdálenost, výšku a zvětšení objektu od objektivu 1
První část výpočtu zvětšení více čoček je stejná jako výpočet zvětšení jedné čočky. Začněte objektivem nejblíže objektu, pomocí rovnice čočky najděte vzdálenost od vytvořeného obrazu a poté pomocí rovnice zvětšení najděte výšku a zvětšení obrazu. Kliknutím sem zobrazíte další výpočty zvětšení jednotlivých čoček.
-
Z našich výpočtů v metodě 1 výše jsme zjistili, že první čočka vytváří obraz tak vysoký jako - 3 996 cm, vzdálenost 33,3 cm za objektivem a při zvětšení - 0, 666.
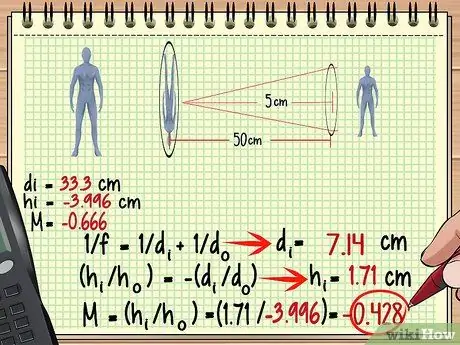
Krok 3. Použijte obraz z prvního objektivu jako objekt z druhého objektivu
Nyní je nalezení zvětšení, výšky a dalších údajů pro druhý objektiv velmi snadné - použijte stejnou metodu, jakou jste použili pro první objektiv, ale tentokrát považujte obraz za objekt. Pamatujte, že vzdálenost obrazu k druhému objektivu není vždy stejná jako vzdálenost objektu k prvnímu objektivu.
-
Ve výše uvedeném příkladu, protože je obraz vytvořen 33,3 cm za prvním objektivem, je vzdálenost 50-33,3 = 16,7 cm před druhým objektivem. Použijme toto měření a ohniskovou vzdálenost druhého objektivu k nalezení obrazu vytvořeného druhým objektivem.
-
- 1/f = 1/dÓ + 1/djá
- 1/5 = 1/16, 7 + 1/djá
- 0, 2 - 0, 0599 = 1/djá
- 0, 14 = 1/djá
- djá = 7, 14 cm
-
-
Nyní můžeme vypočítat hjá a M pro druhý objektiv:
-
- (hjá/hÓ) = -(djá/dÓ)
- (hjá/-3, 996) = -(7, 14/16, 7)
- hjá = -(0, 427) x -3, 996
- hjá = 1,71 cm
- M = (vjá/hÓ)
- M = (1, 71/-3, 996) = - 0, 428
-
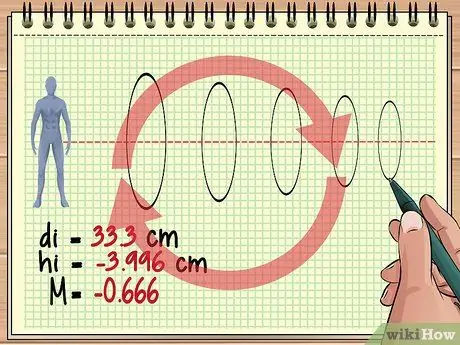
Krok 4. Pokračujte ve výpočtu takto pro další čočky
Tento základní přístup je stejný, pokud jsou před objektem seřazené tři, čtyři nebo stovky čoček. U každého objektivu zvažte obrázek předchozího objektivu jako objekt a pomocí rovnice objektivu a rovnice zvětšení najděte požadovanou odpověď.
Mějte na paměti, že každý následující objektiv může průběžně invertovat vytvořený obraz. Například hodnota zvětšení, kterou jsme získali dříve (-0, 428), naznačuje, že obraz, který uvidíme, je přibližně 4/10 skutečné velikosti objektu, ale kolmý, protože obraz z předchozí čočky je převrácený
Tipy
- Dalekohled obvykle poskytuje vysvětlení specifikací zvětšení ve formě násobku jiného čísla. Dalekohled lze například zadat jako 8x25 nebo 8x40. Když je to takto napsáno, první číslo je zvětšení dalekohledu. Nezáleží na tom, i když v uvedeném příkladu jsou obě čísla různě velká, oba dalekohledy mají zvětšení 8krát. Druhé číslo udává, jak jasný bude obraz tvořen dalekohledem.
- Pamatujte, že u lupy s jedním objektivem bude zvětšení záporné, pokud je vzdálenost objektu větší než ohnisková vzdálenost čočky. To neznamená, že vytvořený obraz bude menší. V tomto případě ke zvětšení stále dochází, ale vytvořený obraz bude pozorovatelem vidět vzhůru nohama (shora dolů).






