- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-02-01 14:12.
- Naposledy změněno 2025-01-23 12:12.
Posun ve fyzice znamená změnu polohy předmětu. Když vypočítáte výtlak, vypočítáte, jak daleko je objekt na základě jeho počátečního a konečného umístění. Vzorec, který použijete pro výpočet výtlaku, závisí na proměnné dané problému. Při výpočtu výtlaku postupujte podle těchto kroků.
Krok
Část 1 z 5: Výpočet výsledného posunutí

Krok 1. Pokud je pro označení počáteční a koncové polohy použita jednotka vzdálenosti, použijte vzorec výsledného posunutí
Přestože se vzdálenost liší od výtlaku, výsledný problém s posunem zjišťuje, kolik kilometrů nebo metrů objekt urazil. Tuto měrnou jednotku použijete k výpočtu posunutí a toho, jak daleko se poloha objektu odchyluje od jeho počátečního bodu.
- Výsledný vzorec posunutí je zapsán jako: S = x²+y². S je posunutí. X je první směr pohybu objektu a Y je druhý směr pohybu objektu. Pokud se váš objekt pohybuje pouze jedním směrem, pak Y = 0.
- Objekt se může pohybovat maximálně ve dvou směrech, protože pohyb podél osy sever/jih nebo východ/západ je považován za neutrální pohyb.

Krok 2. Spojte body v pořadí pohybu a označte je od A-Z
Pomocí pravítka nakreslete přímku z bodu do bodu.
- Nezapomeňte také spojit svůj počáteční bod s koncovým bodem pomocí přímky. Toto je výtlak, který vypočítáme.
- Pokud se například objekt pohybuje na východ 300 m a na sever 400 m, vytvoří pravý trojúhelník. AB bude první částí trojúhelníku a BC bude druhou nohou. AC bude přepona trojúhelníku a jeho velikost je posunutí objektu. V tomto případě jsou dva směry východ a sever.

Krok 3. Zadejte hodnoty pro x² a y²
Nyní, když znáte dva směry pohybu vašeho objektu, zadejte hodnoty do příslušných proměnných.
Například x = 300 a y = 400. Váš vzorec by měl vypadat takto: S = 300² + 400²
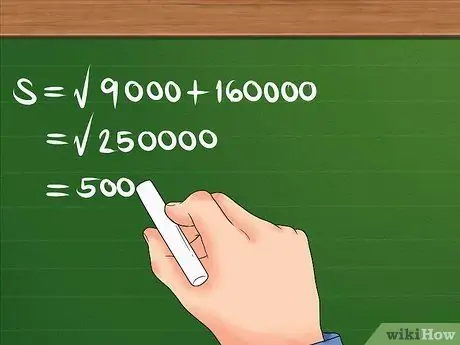
Krok 4. Vypočítejte vzorec pomocí pořadí operací
Nejprve odmocněte 300 a 400, poté je sečtěte a najděte odmocninu součtu.
Například: S = 90000 + 160000. S = 250000. S = 500. Nyní víte, že výtlak je 500 m
Část 2 z 5: Když jsou známy rychlost a čas

Krok 1. Použijte tento vzorec, když vám problém řekne rychlost objektu a čas, který to zabere
Některé matematické úlohy vám neřeknou, jak daleko nebo jak rychle se předmět pohybuje. Pomocí této velikosti času a rychlosti můžete vypočítat výtlak.
-
V tomto případě vzorec bude: S = 1/2 (u + v) t.
U = počáteční rychlost objektu, nebo jak rychle se objekt začne pohybovat v určitém směru. V = konečná rychlost objektu, nebo jak rychle se objekt pohybuje směrem ke svému konečnému umístění. T = doba, za kterou objekt dosáhne svého konečného umístění.
- Příklad: Auto jede po silnici po dobu 45 sekund (požadovaný čas). Vůz se stáčí na západ rychlostí 20 m/s (počáteční rychlost) a na konci silnice je jeho rychlost 23 m/s (konečná rychlost). Vypočítejte výtlak na základě těchto faktorů.

Krok 2. Zadejte požadovanou rychlost a čas do příslušných proměnných
Nyní, když víte, jak daleko se auto pohybuje, jak rychle se auto pohybuje na začátku a na konci, můžete zjistit vzdálenost od počátečního místa do konečného umístění.
Váš vzorec by měl vypadat takto: S = 1/2 (20 + 23) 45

Krok 3. Vypočítejte vzorec poté, co hodnoty vložíte na správné místo
Nezapomeňte dodržovat pořadí operací, jinak budou mít posunutí za následek velmi odlišné hodnoty.
- U tohoto vzorce nezáleží na tom, jestli omylem prohodíte počáteční a koncovou rychlost. Protože budete tato čísla nejprve sčítat, nezáleží na tom, kde jsou v závorkách. U jiných vzorců však bude mít změna počáteční a konečné rychlosti za následek různé hodnoty posunutí.
- Váš vzorec by měl vypadat takto: S = 1/2 (43) 45. Nejprve rozdělte 43 na 2, což má za následek 21, 5. Poté vynásobte 21, 5 krát 45, takže výsledek je 967,5 metru. 967, 5 je velikost vašeho výtlaku neboli toho, jak daleko se vaše auto posunulo od počátečního bodu.
Část 3 z 5: Když jsou známy počáteční rychlost, zrychlení a čas
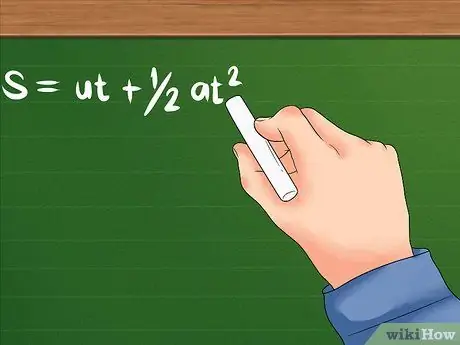
Krok 1. Upravený vzorec použijte, pokud je kromě počáteční rychlosti a času známé i zrychlení
Některé otázky vám řeknou pouze to, jak rychle se objekt pohybuje na začátku, jak rychle se objekt začíná zrychlovat a jak daleko se objekt pohybuje. Budete potřebovat následující vzorec.
- Vzorec pro tento problém je: S = ut + 1/2at². U stále udává počáteční rychlost; a je zrychlení objektu, nebo jak rychle se jeho rychlost začíná měnit. T může znamenat čas potřebný ke zrychlení objektu nebo určitý čas. Oba budou používat časové jednotky, jako jsou sekundy, hodiny a další.
- Předpokládejme, že auto pohybující se rychlostí 25 m/s (počáteční rychlost) začne zrychlovat na 3 m/s2 (zrychlení) po dobu 4 sekund (čas). Jaký je výtlak vozu po 4 sekundách?

Krok 2. Zadejte hodnoty do vzorce
Na rozdíl od předchozího vzorce je zde zastoupena pouze počáteční rychlost, proto nezapomeňte zadat správná data.
Na základě výše uvedených vzorových dat bude váš vzorec vypadat takto: S = 25 (4) + 1/2 (3) 4². Pomůže vám přidat závorky kolem velikosti zrychlení a času, což vám pomůže čísla oddělit
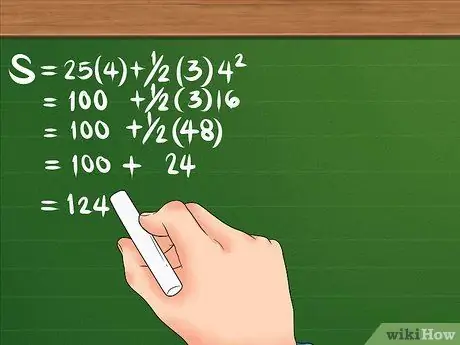
Krok 3. Vypočítejte posunutí provedením ve správném pořadí operací
Rychlý způsob, jak si zapamatovat sled operací, je oslí můstek Kur ir Kua ci Kadang Ba wa Juragan Turtles. To představuje správné pořadí: závorky, čtverce, násobení, dělení, sčítání a odčítání.
Podívejme se znovu na vzorec: S = 25 (4) + 1/2 (3) 4². Za prvé, čtverec 4, výsledek je 16. Potom vynásobte 16 čísly 3, takže 48; pak také vynásobte 25 čtyřmi, abyste získali 100. Rozdělte 48 na 2, abyste vytvořili 24. Vaše rovnice by měla vypadat takto: S = 100 + 24. Jakmile sečtete obě dohromady, výtlak je 124 metrů
Část 4 z 5: Výpočet úhlového posunutí

Krok 1. Najděte úhlové posunutí, když se objekt pohybuje po kruhové dráze
Ačkoli budete stále počítat posunutí pomocí přímky, budete muset najít rozdíl mezi počátečním a koncovým umístěním objektu při jeho pohybu po kruhové dráze.
- Představte si dívku sedící na kolotoči. Jak se točí kolotočem, bude se pohybovat po kruhové dráze. Úhlový posun se pokouší najít nejkratší vzdálenost mezi počátečním a konečným umístěním, když se objekt nepohybuje v přímce.
- Vzorec pro úhlové posunutí je: = S/r, kde S je lineární posun, r je poloměr a je úhlový posun. Lineární posunutí je to, jak daleko se objekt pohybuje po oblouku. Poloměr je vzdálenost objektu od středu kruhu. Úhlové posunutí je hodnota, kterou chceme najít.

Krok 2. Zapojte lineární posun a poloměr do rovnice
Pamatujte, že poloměr je vzdálenost od středu kruhu; některé problémy vám řeknou průměr kruhu, který musí být dělen 2, aby se našel poloměr.
- Zde je příklad problému: Dívka jede na kolotoči. Sedadlo je 1 metr od středu kruhu (poloměru). Pokud se dívka pohybuje po obloukové dráze 1,5 metru (lineární posun), jaký je její úhlový posun?
- Vaše rovnice bude vypadat takto: = 1,5/1.
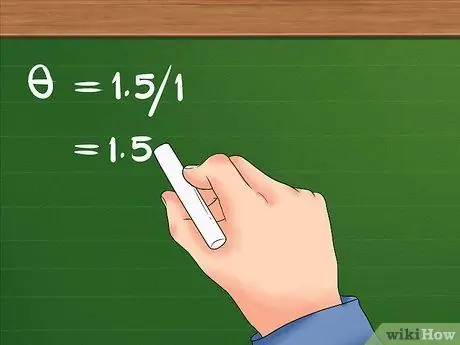
Krok 3. Vydělte lineární posunutí poloměrem
Toto rozdělení bude mít za následek úhlové posunutí objektu.
- Po dělení 1,5 na 1 je výsledkem 1,5. Uhlový posun dívky je 1,5 radiány.
- Protože úhlové posunutí měří, jak moc se předmět otáčí ze své původní polohy, měl by být měřen jako úhel, nikoli jako vzdálenost. Radian je jednotka používaná k měření úhlů.
Část 5 z 5: Porozumění migraci
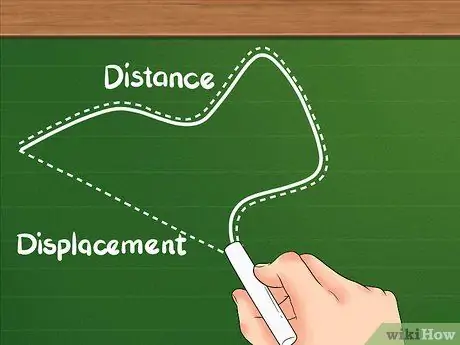
Krok 1. Vězte, že vzdálenost má jinou definici než posunutí
Vzdálenost ukazuje, jak daleko je celková vzdálenost, kterou objekt urazil.
- Vzdálenost je často známá jako skalární veličina. Vzdálenost udává vzdálenost, kterou objekt urazil bez ohledu na směr objektu.
- Pokud například půjdete 2 kroky na východ, 2 kroky na jih, 2 kroky na západ a poté 2 kroky na sever, vrátíte se do výchozí polohy. I když jste celkem prošli vzdálenost Jen 10 kroků odtud přestěhovat se 0 kroků, protože vaše konečné umístění je stejné jako vaše výchozí umístění (vaše cesta připomíná pole).

Krok 2. Pochopte, že posun je rozdíl mezi dvěma místy
Posun není celkový součet pohybu jako vzdálenost; směny se zaměřují na oblast mezi vaší počáteční a koncovou polohou.
- Posun se nazývá vektorová veličina a ukazuje změnu polohy objektu zvážením směru pohybu objektu.
- Například jdete na východ po 5 schodech. Pokud se vrátíte o 5 kroků zpět na západ, budete se pohybovat v opačném směru než vaše původní místo. I když jste překonali 10 kroků, vaše pozice se nezměnila; váš výtlak je 0 kroků.

Krok 3. Pamatujte si slova dopředu a dozadu, když se snažíte představit si posun
Pohyb v opačném směru eliminuje posunutí předmětu.
Představte si fotbalového trenéra tam a zpět na okraji. Když na hráče křičel, několikrát přešel zleva doprava. Pokud ho sledujete, jak se pohybuje zleva doprava, sledujete celkovou vzdálenost, kterou urazil. Předpokládejme však, že trenér přestane mluvit s quarterbackem na vedlejší kolej. Pokud je před přesunem v jiném bodě, než ve kterém byl původně, pak pozorujete pohyb trenéra

Krok 4. Vězte, že výtlak se měří přímou cestou, nikoli kruhovou
Chcete -li najít posunutí, musíte najít nejkratší a nejefektivnější způsob výpočtu rozdílu mezi dvěma body.
- Kruhová cesta vás zavede z výchozího místa do konečného, ale není to nejkratší cesta. Abyste si to mohli lépe představit, představte si, že jdete po přímce a narazíte na sloup. Tento pilíř nemůžete prorazit, a tak ho obejdete. Přestože je vaše konečná pozice stejná, jako kdybyste prorazili pilíř, budete k dosažení tohoto cíle potřebovat další kroky.
- Přestože posunutí představuje přímou cestu, vězte, že můžete změřit posunutí objektu, který je v současné době pohybovat po kruhové dráze. Toto posunutí se nazývá úhlové posunutí a lze jej vypočítat nalezením nejkratší cesty z počátečního umístění do konečného umístění.

Krok 5. Vězte, že výtlak může být na rozdíl od vzdálenosti záporný
Pokud je vašeho konečného umístění dosaženo pohybem v opačném směru, než je váš původní směr, pak je váš výtlak záporný.
- Například jdeme 5 kroků na východ a pak 3 kroky na západ. Přestože se výpočtem přesunete o 2 kroky z výchozího místa, váš posun je -2, protože se pohybujete opačným směrem. Vaše vzdálenost bude vždy kladná, protože nemůžete počítat zpět v krocích, kilometrech atd.
- Negativní posunutí neznamená, že se posunutí sníží. Negativní znamená, že směr je opačný.

Krok 6. Uvědomte si, že někdy vzdálenost a výtlak mohou být stejné
Pokud půjdete rovně po 25 schodech a zastavíte, ujetá vzdálenost se bude rovnat výtlaku z vašeho původního místa.
- To platí pouze v případě, že se pohybujete z jednoho místa ze svého počátečního umístění po přímce. Žijete například v San Francisku v Kalifornii a získáte novou práci v Las Vegas v Nevadě. Musíte se přestěhovat do Las Vegas, abyste byli blízko své práci. Pokud si sednete do letadla, které letí rovný ze San Franciska do Las Vegas urazíte stejnou vzdálenost a výtlak x.
- Pokud však pojedete ze San Franciska do Las Vegas, urazíte vzdálenost x, ale urazíte vzdálenost y. Protože řízení automobilu má obvykle různé směry (východně od této silnice, západně od této silnice), budete cestovat delší vzdálenosti, než je nejkratší vzdálenost mezi těmito dvěma městy.






