- Autor Jason Gerald [email protected].
- Public 2024-01-15 08:11.
- Naposledy změněno 2025-01-23 12:14.
Hodnota P je statistické měření, které vědcům pomáhá určit, zda je jejich hypotéza správná. Hodnota P se používá k určení, zda jsou výsledky jejich experimentu v rozmezí hodnot, které jsou pro studované věci normální. Obvykle, pokud hodnota P souboru dat klesne pod určitou předem stanovenou hodnotu (například 0,05), vědci odmítnou nulovou hypotézu svého experimentu - jinými slovy vyloučí hypotézu, kde experimentální proměnná má žádný významný vliv na výsledek. Dnes se hodnoty p obvykle nacházejí v referenčních tabulkách výpočtem hodnoty chi na druhou.
Krok

Krok 1. Určete očekávané výsledky vašeho experimentu
Obvykle, když vědci provádějí experiment a zkoumají výsledky, mají již předem představu o normálních nebo běžných výsledcích. To může být založeno na výsledcích předchozích experimentů, spolehlivých souborech pozorovacích dat, vědecké literatuře a/nebo jiných zdrojích. Pro svůj experiment určete očekávaný výsledek a zapište jej jako číslo.
Příklad: Předpokládejme, že předchozí studie ukázala, že na národní úrovni byly lístky na překročení rychlosti vydávány častěji červeným autům než modrým vozům. Předpokládejme, že průměrný výsledek na národní úrovni ukazuje poměr 2: 1, přičemž poměr červených aut je vyšší. Chceme zjistit, zda stejnou tendenci dostává i policie v našem městě, a to rozborem jízdenky za překročení rychlosti vydané policií v našem městě. Pokud bychom vzali náhodný vzorek 150 lístků na překročení rychlosti, které byly dány červeným i modrým autům v našem městě, očekávali bychom 100 pro červené auto a 50 pro modrá auta, pokud policejní jednotka v našem městě dá lístek podle srovnání na národní úrovni.

Krok 2. Určete svá experimentální pozorování
Nyní, když jste určili očekávanou hodnotu, můžete spustit experiment a najít skutečnou hodnotu (nebo pozorování). Výsledek opět zapište jako číslo. Pokud manipulujeme s některými experimentálními podmínkami a pozorované výsledky se liší od očekávaných výsledků, existují dvě možnosti: buď se to stalo náhodou, nebo to byla naše manipulace s experimentálními proměnnými, která způsobila tento rozdíl. Účelem nalezení hodnoty p je v zásadě určit, zda se pozorované výsledky liší od očekávaných výsledků do bodu, kdy nulovou hypotézu-hypotézu, že neexistuje žádný vztah mezi experimentální proměnnou a pozorovanými výsledky-nelze odmítnout.
Příklad: Předpokládejme, že v našem městě náhodně vybereme 150 lístků na překročení rychlosti, které budou uděleny červeným i modrým autům. Dostaneme 90 lístek na červené auto a 60 pro modré auto. To se liší od výsledku, který jsme očekávali, tj 100 a 50. Způsobila naše experimentální manipulace (v tomto případě změna zdroje dat z národní na místní) nějakou změnu ve výsledcích, nebo naše městská policie měla stejné tendence jako národní úroveň a my jsme jen pozorovali shodu? Hodnota p nám to pomůže určit.

Krok 3. Určete stupně volnosti pro váš experiment
Stupně volnosti jsou měřítkem míry variability ve studii, která je dána počtem zkoumaných kategorií. Rovnice pro stupně volnosti je Stupně volnosti = n-1, kde n je počet kategorií nebo proměnných analyzovaných ve vašem experimentu.
-
Příklad: Náš experiment má dvě kategorie výsledků: jednu pro červené auto a jednu pro modré auto. V našem experimentu tedy máme 2-1 = 1 stupeň volnosti.
Pokud porovnáme červená, modrá a zelená auta, budeme mít
Krok 2. stupně volnosti a tak dále.

Krok 4. Porovnejte očekávané výsledky s pozorovanými výsledky pomocí chi na druhou
Chi na druhou (psáno x2) je číselná hodnota, která měří rozdíl mezi očekávanými a pozorovanými hodnotami z experimentu. Rovnice pro chi na druhou je: X2 = ((o-e)2/E), kde o je pozorovaná hodnota a e je očekávaná hodnota. Sečtěte výsledky této rovnice pro všechny možné výsledky (viz níže).
- Všimněte si, že tato rovnice používá operátor (sigma). Jinými slovy, musíte vypočítat ((| o-e | -.05)2/e) pro každý možný výsledek pak sečtěte výsledky, abyste získali chi druhou mocninu. V našem příkladu máme dva výsledky - auto, které dostane červený nebo modrý lístek. Můžeme tedy vypočítat ((o-e)2/e) dvakrát - jednou pro červené auto a jednou pro modré auto.
-
Příklad: Vložíme naše očekávané hodnoty a pozorování do rovnice x2 = ((o-e)2/E). Pamatujte, že kvůli sigma operátorovi musíme vypočítat ((o-e)2/e) dvakrát - jednou pro červené auto a jednou pro modré auto. Kroky zpracování jsou následující:
- X2 = ((90-100)2/100) + (60-50)2/50)
- X2 = ((-10)2/100) + (10)2/50)
- X2 = (100/100) + (100/50) = 1 + 2 = 3.

Krok 5. Vyberte úroveň významnosti
Nyní, když známe stupně volnosti naší experimentální soupravy a chí kvadratickou hodnotu, zbývá jen poslední věc, kterou musíme udělat, než můžeme najít naši hodnotu p-musíme určit úroveň významnosti. Úroveň významnosti je v zásadě měřítkem toho, jak jsme si svými výsledky jisti - nízká úroveň významnosti odpovídá nízké pravděpodobnosti, že výsledek experimentu byl způsoben náhodou a naopak. Úroveň významnosti je zapsána jako desetinné číslo (např. 0,01), což odpovídá procentní šanci, že výsledek experimentu byl způsoben náhodou (v tomto případě 1%).
- Podle konvence vědci obvykle stanovili hodnotu významnosti pro své experimenty na 0,05 nebo 5 procent. To znamená, že experimentální výsledky, které odpovídají této hladině významnosti, mají maximálně 5% šanci na shodu. Jinými slovy, existuje 95% šance, že výsledky jsou způsobeny vědcovou manipulací s experimentálními proměnnými, a nikoli náhoda. U většiny experimentů se 95% spolehlivost vztahu mezi těmito dvěma proměnnými považuje za úspěšnou při demonstraci vztahu mezi těmito dvěma proměnnými.
- Příklad: U našeho příkladu s červeným a modrým autem se pojďme řídit vědeckou dohodou a určit naši úroveň významnosti 0, 05.
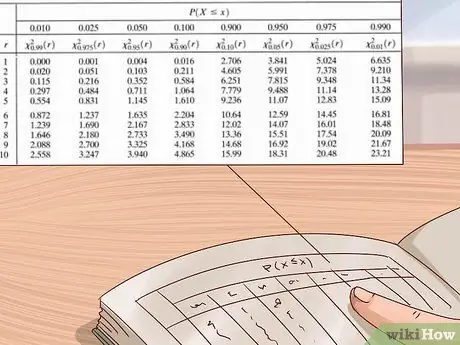
Krok 6. K odhadnutí hodnoty p použijte čtvercovou distribuční tabulku čchi
Vědci a statistici používají velké tabulky hodnot k výpočtu hodnot p pro své experimenty. Tato tabulka je obvykle psána tak, že svislá osa vlevo ukazuje stupně volnosti a vodorovná osa nahoře ukazuje hodnoty p. Tuto tabulku použijte tak, že nejprve najdete své stupně volnosti a poté čtete řádky zleva doprava, dokud nenajdete první hodnotu, která je větší než vaše hodnota chi na druhou. Podívejte se na hodnotu p v horní části sloupce-vaše hodnota p je mezi touto hodnotou a další největší hodnotou (správná hodnota je nalevo od ní).
- Distribuční tabulky Chi square jsou k dispozici z různých zdrojů - lze je snadno najít online nebo v učebnicích vědy nebo statistiky. Pokud ho nemáte, použijte tabulku uvedenou na fotografii výše nebo bezplatnou online tabulku, jako je ta, kterou zde poskytuje medcalc.org.
-
Příklad: Naše chi na druhou je 3. Použijme tedy čtvercovou distribuční tabulku chi na fotografii výše k nalezení přibližné hodnoty p. Protože víme, že náš experiment má pouze
Krok 1. stupně volnosti, začneme od nejvyšší tabulky. V této řadě jdeme zleva doprava, dokud nenajdeme hodnotu vyšší než
Krok 3. - naše hodnota chi na druhou. První hodnota, kterou najdeme, je 3,84. Při pohledu na tento sloupec vidíme, že odpovídající hodnota p je 0,05. To znamená, že naše hodnota p je mezi 0,05 a 0,1 (další největší p-hodnota v tabulce).

Krok 7. Rozhodněte se, zda svou nulovou hypotézu odmítnete nebo obhájíte
Protože jste pro svůj experiment našli přibližnou hodnotu p, můžete se rozhodnout, zda nulovou hypotézu svého experimentu odmítnete (jako připomenutí, toto je hypotéza, že experimentální proměnná, kterou jste manipulovali, neměla žádný vliv na výsledky, které jste pozorovali). Pokud je vaše hodnota p nižší než hodnota významnosti, gratulujeme-dokázali jste, že existuje vysoká pravděpodobnost, že existuje vztah mezi proměnnými, se kterými jste manipulovali, a vašimi pozorováními. Pokud je vaše hodnota p větší než hodnota významnosti, nemůžete s jistotou říci, že výsledky, které pozorujete, jsou výsledkem pouhé náhody nebo manipulace s vaším experimentem.
- Příklad: Naše hodnota p je mezi 0,05 a 0,1. To znamená, že v žádném případě není menší než 0,05, takže bohužel nemůže naši nulovou hypotézu odmítnout. To znamená, že nedosahujeme minimálního 95% limitu spolehlivosti, který jsme stanovili, takže lze říci, že policie v našem městě dává jízdenky na červená a modrá auta v poměru, který je zcela odlišný od celostátního průměru.
- Jinými slovy, existuje 5-10% šance, že naše pozorování nejsou výsledkem změny polohy (analýza našeho města, a ne celé části), ale jsou to náhody. Jelikož hledáme pravděpodobnost menší než 5%, nemůžeme říci, že ano přesvědčený že policie v našem městě má tendenci vydávat lístky na červená auta - existuje malá, ale statisticky velmi odlišná možnost, že tuto tendenci nemají.
Tipy
- Vědecká kalkulačka výpočty výrazně usnadní. Kalkulačky můžete také vyhledat online.
- Hodnoty p můžete vypočítat pomocí několika počítačových programů, včetně běžně používaného tabulkového softwaru a specializovanějšího statistického softwaru.






