3 způsoby výpočtu tlaku par

2024 Autor: Jason Gerald | [email protected]. Naposledy změněno: 2024-02-01 14:12

Nechali jste někdy láhev vody na pár hodin na prudkém slunci a slyšeli jste při jejím otevření mírný „syčící“zvuk? Je to dáno principem, kterému se říká tlak par. V chemii je tlak par tlak vyvíjený stěnami uzavřené nádoby, když se v ní chemická látka odpařuje (mění se v plyn). Chcete-li zjistit tlak par při dané teplotě, použijte Clausius-Clapeyronovu rovnici: ln (P1/P2) = (ΔH_pára/R) ((1/T2) - (1/T1)).

Krok

Metoda 1 ze 3: Použití Clausius-Clapeyronovy rovnice

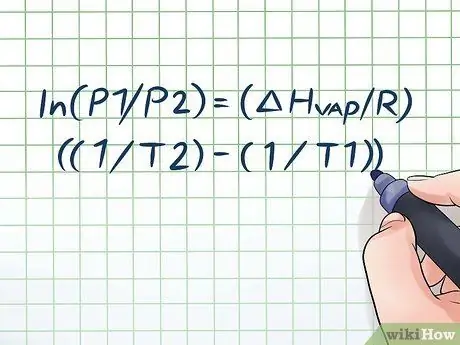
Krok 1. Zapište Clausius-Clapeyronovu rovnici

Vzorec použitý pro výpočet tlaku par se změnou tlaku par v průběhu času se nazývá Clausius -Clapeyronova rovnice (pojmenovaná podle fyziků Rudolfa Clausia a Benoîta Paula míle Clapeyrona.) Toto je v podstatě vzorec, který budete potřebovat k vyřešení většiny typů problémů Otázky týkající se tlaku par se často nacházejí na hodinách fyziky a chemie. Vzorec je následující: ln (P1/P2) = (ΔH_pára/R) ((1/T2) - (1/T1)). V tomto vzorci proměnné představují:

• H_pára:

  Entalpie odpařování kapaliny. Tuto entalpii obvykle najdete v tabulce na konci učebnice chemie.

• R:

  Skutečná/univerzální plynová konstanta nebo 8,314 J/(K × Mol).

• Q1:

  Teplota, při které je znám tlak par (nebo počáteční teplota).

• T2:

  Teplota, při které je tlak par neznámý/chtěl být nalezen (nebo konečná teplota).

• P1 a P2:

  Tlak páry při teplotách T1, respektive T2.

Krok 2. Zadejte proměnné, které znáte

Clausius-Clapeyronova rovnice vypadá komplikovaně, protože obsahuje mnoho různých proměnných, ale ve skutečnosti to není tak obtížné, pokud máte správné informace. Většina základních problémů s tlakem par bude obsahovat dvě hodnoty teploty a jednu hodnotu tlaku nebo dvě hodnoty tlaku a jednu hodnotu teploty - jakmile na to přijdete, řešení této rovnice je velmi snadné.

• Řekněme například, že nám bylo řečeno, že máme nádobu plnou kapaliny o 295 K, jejíž tlak par je 1 atmosféra (atm). Naše otázka zní: Jaký je tlak par při 393 K? Máme dvě hodnoty teploty a jednu hodnotu tlaku, takže ostatní hodnoty tlaku můžeme najít pomocí Clausius-Clapeyronovy rovnice. Připojením našich proměnných získáme ln (1/P2) = (ΔH_pára/R) ((1/393) - (1/295)).
• U Clausius-Clapeyronovy rovnice musíte vždy použít hodnotu teploty Kelvin. Můžete použít libovolnou hodnotu tlaku, pokud jsou hodnoty pro P1 a P2 stejné.

Krok 3. Zadejte své konstanty

Clausius-Clapeyronova rovnice má dvě konstanty: R a H_pára. R se vždy rovná 8,314 J/(K × Mol). Nicméně, H_pára (entalpie odpařování) závisí na látce, jejíž tlak par hledáte. Jak bylo uvedeno výše, hodnoty H obvykle najdete_pára pro různé látky v zadní části učebnice chemie nebo fyziky nebo online (jako například zde.)

• V našem případě předpokládejme, že naše kapalina je čistá voda.

  Podíváme -li se do tabulky na hodnoty H_pára, zjišťujeme, že H_pára čistá voda je asi 40,65 KJ/mol. Protože naše hodnota H je v joulech, a ne v kilojoulech, můžeme ji převést na 40 650 J/mol.

• Když zapojíme naše konstanty, dostaneme ln (1/P2) = (40 650/8, 314) ((1/393) - (1/295)).

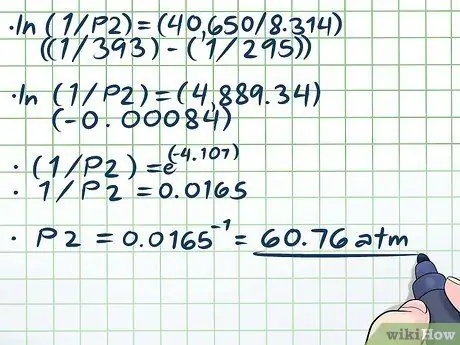
Krok 4. Vyřešte rovnici

Jakmile do rovnice zahrnete všechny proměnné kromě té, kterou hledáte, pokračujte v řešení rovnice podle pravidel běžné algebry.

• Jediná obtížná část řešení naší rovnice (ln (1/P2) = (40 650/8, 314) ((1/393) - (1/295))) je řešení přirozeného logu (ln). Chcete -li odstranit přirozený log, použijte obě strany rovnice jako exponenty pro matematickou konstantu e. Jinými slovy, ln (x) = 2 → e^{ln (x)} = e² → x = e².

• Nyní vyřešíme naši rovnici:
• ln (1/P2) = (40 650/8, 314) ((1/393) - (1/295))
• ln (1/P2) = (4889, 34) (-0, 00084)
• (1/P2) = e^{(-4, 107)}
• 1/P2 = 0,0165

• P2 = 0,0165^-1 = 60, 76 atm.

  To dává smysl - v uzavřené nádobě při zvýšení teploty na téměř 100 stupňů (téměř na 20 stupňů nad bod varu) vznikne velké množství páry, čímž se tlak rychle zvýší.

Metoda 2 ze 3: Zjištění tlaku par s rozpuštěným roztokem

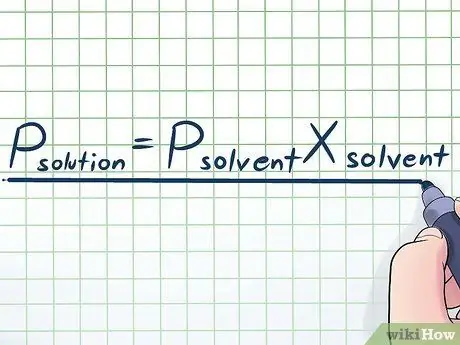
Krok 1. Zapište si Raoultův zákon

V reálném životě jen zřídka pracujeme s čistou tekutinou - obvykle pracujeme s kapalinou, která je směsí několika různých látek. Některé z nejčastěji používaných směsí se vyrábějí rozpuštěním malého množství určité chemikálie zvané rozpuštěná látka v mnoha chemikáliích nazývaných rozpouštědla za vzniku roztoku. V těchto případech je užitečné znát rovnici nazvanou Raoultův zákon (pojmenovanou podle fyzika François-Marie Raoult), která je napsána takto: P_solute= P_solventníX_solventní. V tomto vzorci proměnné představují;

• P_solute:

  Tlak páry celého roztoku (všechny prvky dohromady)

• P_solventní:

  Tlak par rozpouštědla

• X_solventní:

  Molární frakce rozpouštědla

• Pokud neznáte pojmy jako zlomek molů, nedělejte si starosti - vysvětlíme je v několika následujících krocích.

Krok 2. Určete rozpouštědlo a rozpuštěnou látku ve vašem roztoku

Než budete moci vypočítat tlak par smíšené kapaliny, musíte identifikovat látky, které používáte. Připomínáme, že roztok vzniká, když se rozpuštěná látka rozpouští v rozpouštědle - chemikálie, která se rozpouští, se vždy nazývá rozpuštěná látka a chemikálie, která ji rozpouští, se vždy nazývá rozpouštědlo.

• Pojďme pracovat pomocí jednoduchých příkladů v této části, abychom ilustrovali koncepty, o kterých diskutujeme. Pro náš příklad řekněme, že chceme zjistit tlak par cukrového sirupu. Cukrový sirup je tradičně cukr rozpustný ve vodě (poměr 1: 1), takže to můžeme říci cukr je naše rozpuštěná látka a voda je naše rozpouštědlo.
• Chemický vzorec pro sacharózu (stolní cukr) je C₁₂H₂₂Ó₁₁. Tento chemický vzorec bude velmi důležitý.

Krok 3. Zjistěte teplotu roztoku

Jak jsme viděli v sekci Clausius Clapeyron výše, teplota kapaliny ovlivní její tlak par. Obecně platí, že čím vyšší je teplota, tím větší je tlak par - jak teplota stoupá, více kapaliny se odpaří a vytvoří páru, čímž se tlak v nádobě zvýší.

V našem případě řekněme, že teplota cukrového sirupu v tomto bodě je 298 K. (asi 25 C).

Krok 4. Najděte tlak par rozpouštědla

Chemické referenční materiály mají obvykle hodnoty tlaku par pro mnoho běžně používaných látek a sloučenin, ale tyto hodnoty tlaku jsou obvykle platné pouze tehdy, má -li látka teplotu 25 C/298 K nebo její teplotu varu. Pokud má vaše řešení jednu z těchto teplot, můžete použít referenční hodnotu, ale pokud ne, budete muset zjistit tlak par při této teplotě.

• Clausius -Clapeyron může pomoci - použijte referenční tlak par a 298 K (25 C) pro P1 a T1.
• V našem příkladu má naše směs teplotu 25 C, takže můžeme snadno použít naši snadnou referenční tabulku. Víme, že při 25 C má voda tlak páry 23,8 mm HG

Krok 5. Najděte molární zlomek svého rozpouštědla

Poslední věc, kterou musíme udělat, než to vyřešíme, je najít molární zlomek našeho rozpouštědla. Nalezení molární frakce je snadné: jednoduše převeďte své sloučeniny na moly a poté najděte procento každé sloučeniny z celkového počtu molů v látce. Jinými slovy, molární zlomek každé sloučeniny je roven (moly sloučeniny)/(celkový počet molů v látce).

• Předpokládejme náš recept na použití cukrového sirupu 1 litr (L) vody a 1 litr sacharózy (cukru).

  V tomto případě musíme zjistit počet molů každé sloučeniny. Za tímto účelem zjistíme hmotnost každé sloučeniny a poté ji pomocí molární hmotnosti látky převedeme na moly.

• Hmotnost (1 L vody): 1 000 gramů (g)
• Hmotnost (1 litr surového cukru): přibližně 1056, 8 g
• Moly (voda): 1 000 gramů × 1 mol/18,015 g = 55,51 mol
• Moly (sacharóza): 1056, 7 gramů × 1 mol/342,2965 g = 3,08 molů (všimněte si, že molární hmotnost sacharosy najdete podle jejího chemického vzorce C₁₂H₂₂Ó₁₁.)
• Celkový počet molů: 55,51 + 3,08 = 58,59 mol
• Molární podíl vody: 55, 51/58, 59 = 0, 947

Krok 6. Dokončete

Nakonec máme vše, co potřebujeme k vyřešení rovnice našeho Raoultova zákona. Tato část je velmi snadná: stačí zadat hodnoty proměnných ve zjednodušené Raoultově rovnici na začátku této části (P_solute = P_solventníX_solventní).

• Zadáním našich hodnot získáme:
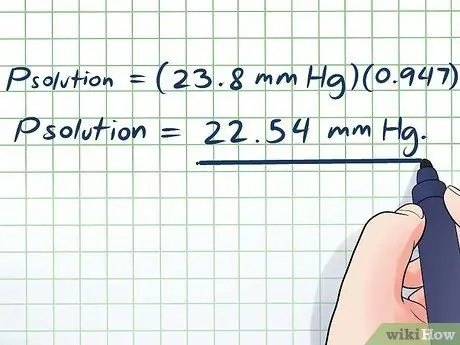
• P_řešení = (23,8 mm Hg) (0, 947)

• P_řešení = 22,54 mm Hg.

  Výsledek dává smysl - v molech je ve velkém množství vody rozpuštěno velmi málo cukru (i když v reálném světě mají obě složky stejný objem), takže tlak par se sníží jen mírně.

Metoda 3 ze 3: Zjištění tlaku páry ve zvláštních případech

Krok 1. Buďte opatrní při podmínkách standardní teploty a tlaku

Vědci často používají sadu hodnot teploty a tlaku jako snadno použitelný „standard“. Tyto hodnoty se nazývají standardní teplota a tlak (nebo STP). Problémy s tlakem par se často týkají podmínek STP, proto je důležité si tyto hodnoty pamatovat. Hodnoty STP jsou definovány jako:

• Teplota: 273, 15 K. / 0 C. / 32 F
• Tlak: 760 mm Hg / 1 atm / 101, 325 kilopascalů

Krok 2. Přeuspořádejte Clausius-Clapeyronovu rovnici, abyste našli další proměnné

V našem příkladu v části 1 jsme viděli, že Clausiova -Clapeyronova rovnice je velmi užitečná pro zjištění tlaku par čistých látek. Ne všechny otázky vás však požádají, abyste hledali P1 nebo P2 - mnoho vás požádá, abyste našli hodnotu teploty nebo někdy dokonce hodnotu H._pára. Naštěstí v těchto případech je správná odpověď jednoduše otázkou přeskupení rovnice tak, aby proměnné, které chcete vyřešit, byly na jedné straně znaménka rovnítka oddělené.

• Řekněme například, že máme neznámou kapalinu s tlakem par 25 torr při 273 K a 150 torr při 325 K a chceme najít entalpii vaporizace této kapaliny (ΔH_pára). Můžeme to vyřešit takto:
• ln (P1/P2) = (ΔH_pára/R) ((1/T2) - (1/T1))
• (ln (P1/P2))/((1/T2) - (1/T1)) = (ΔH_pára/R)
• R × (ln (P1/P2))/((1/T2) - (1/T1)) = H_pára Nyní zadáme naše hodnoty:
• 8, 314 J/(K × Mol) × (-1, 79)/(-0, 00059) = H_pára
• 8, 314 J/(K × Mol) × 3033, 90 = H_pára = 25,223, 83 J/mol

Krok 3. Vypočítejte tlak par rozpuštěné látky, když látka produkuje páru

V našem příkladu Raoultova zákona výše, naše rozpuštěná látka, cukr, nevyvíjí za normálních teplot žádný tlak (přemýšlejte - kdy jste naposledy viděli, jak se ve vaší horní skříňce odpařuje mísa cukru?) Když však vaše rozpuštěná látka odpařit, ovlivní to váš tlak par. Vyúčtujeme to pomocí upravené verze rovnice Raoultova zákona: P_řešení = (Str_sloučeninaX_sloučenina) Symbol sigma (Σ) znamená, že k získání odpovědi potřebujeme pouze sečíst všechny tlaky par různých sloučenin.

• Řekněme například, že máme roztok vyrobený ze dvou chemikálií: benzenu a toluenu. Celkový objem roztoku je 12 mililitrů (ml); 60 ml benzenu a 60 ml toluenu. Teplota roztoku je 25 ° C a tlaky par každé z těchto chemikálií při 25 ° C jsou 95,1 mm Hg pro benzen a 28,4 mm Hg pro toluen. S těmito hodnotami najděte tlak par roztoku. Můžeme to provést následujícím způsobem pomocí standardních hodnot hustoty, molární hmotnosti a tlaku par pro naše dvě chemikálie:
• Hmotnost (benzen): 60 ml = 0,060 l a krát 876,50 kg/1 000 l = 0,053 kg = 53 g
• Hmotnost (toluen): 0,060 l a krát 866, 90 kg/1 000 l = 0,052 kg = 52 g
• Mol (benzen): 53 g × 1 mol/78, 11 g = 0,679 mol
• Moly (toluen): 52 g × 1 mol/92, 14 g = 0,564 mol
• Celkový počet molů: 0,679 + 0,564 = 1,243
• Molární frakce (benzen): 0,679/1, 243 = 0,546
• Molární frakce (toluen): 0,564/1, 243 = 0,454
• Řešení: P_řešení = P_benzenX_benzen + P_toluenX_toluen
• P_řešení = (95,1 mm Hg) (0, 546) + (28,4 mm Hg) (0, 454)
• P_řešení = 51,92 mm Hg + 12,89 mm Hg = 64, 81 mm Hg

Tipy

• Chcete -li použít Clausius Clapeyronovu rovnici výše, musí být teplota měřena v Kelvinech (psáno jako K). Pokud máte teplotu ve stupních Celsia, musíte ji převést pomocí následujícího vzorce: T_k = 273 + T_C
• Výše uvedené metody lze použít, protože energie je přesně úměrná množství aplikovaného tepla. Teplota kapaliny je jediným faktorem prostředí, který ovlivňuje tlak par.