- Autor Jason Gerald [email protected].
- Public 2023-12-16 11:01.
- Naposledy změněno 2025-01-23 12:14.
Pro většinu lidí jsou zlomky první komplikované výpočty, se kterými se lze setkat. Pojem zlomků je poměrně obtížný a vyžaduje, abyste se k tomu naučili speciální podmínky. Protože zlomky mají speciální pravidla pro sčítání, odčítání, násobení a dělení, mnoho lidí z toho má zmatek. S velkou praxí se však každý může naučit a dokončit výpočty týkající se zlomků.
Krok
Metoda 1 z 5: Porozumění zlomkům
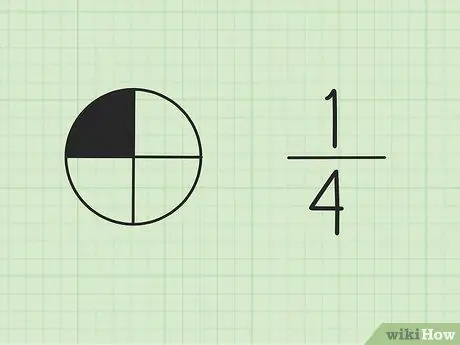
Krok 1. Pochopte, že zlomky jsou součástí celku
Číslo nahoře se nazývá čitatel a představuje počet částí součtu. Číslo ve spodní části se nazývá jmenovatel, což představuje celkový počet částí.
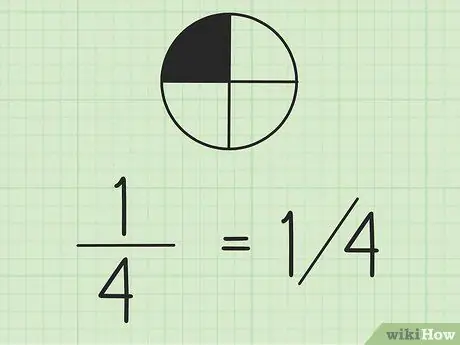
Krok 2. Mějte na paměti, že zlomky můžete psát pomocí lomítek
Číslo vlevo je čitatel a číslo vpravo jmenovatel. Pokud pracujete se zlomky na stejném řádku, je dobré napsat čitatele nad jmenovatele.
Pokud si například vezmete jeden ze čtyř plátků pizzy, máte pizzu. Pokud máte 7/3 pizzy, znamená to, že máte dvě celé pizzy plus 1 ze 3 plátků pizzy
Metoda 2 z 5: Rozdíl mezi smíšenými a jednoduchými zlomky

Krok 1. Pochopte, že smíšená čísla se skládají z celých čísel a zlomků, například 2 1/3 nebo 45 1/2
Obvykle musíte převést smíšená čísla na jednodušší formu, kterou chcete sčítat, odčítat, násobit nebo dělit.

Krok 2. Změňte smíšené číslo vynásobením celého čísla jmenovatelem ve zlomku a poté přidáním čitatele
Výsledek zapište jako čitatel, zatímco jmenovatel se nezmění.
Chcete -li například převést 2 1/3 na jednoduchý zlomek, vynásobte 2 x 3, poté přidejte 1 a získejte 7/3

Krok 3. Převod jednoduchých zlomků na smíšená čísla dělením čitatele jmenovatelem
Celý výsledek dělení je zapsán jako celé číslo a zbytek dělení je zapsán jako čitatel zlomku. Jmenovatel se nemění.
Chcete -li například převést 7/3 na smíšené číslo, rozdělte 7 na 3 a získejte 2 se zbytkem 1. Smíšené číslo je tedy 2 1/3. Jednoduché zlomky lze převést na smíšená čísla, pouze pokud je čitatel větší než jmenovatel
Metoda 3 z 5: Sčítání a odčítání zlomků
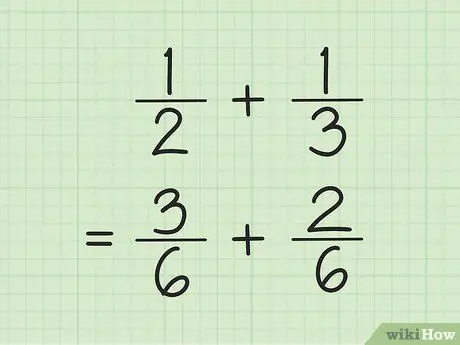
Krok 1. Najděte společného jmenovatele pro sčítání a odčítání zlomků
Trik, vynásobte čísla ve jmenovateli a poté vynásobte každého čitatele číslem použitým k nalezení jmenovatele. Někdy můžete LCM (nejmenší společný násobek) pro jmenovatele najít vynásobením jmenovatelů navzájem.
Chcete -li například přidat a 1/3, nejprve najděte LCM (nejmenší společný násobek) dvou jmenovatelů vzájemným vynásobením. Vynásobením 2 a 3 získáte LCM 6. Vynásobením 1 číslem 3 získáte 3 jako nového čitatele prvního zlomku. Vynásobením 1 číslem 2 získáte 2 jako nového čitatele druhého zlomku. Vaše nové zlomky jsou 3/6 a 2/6
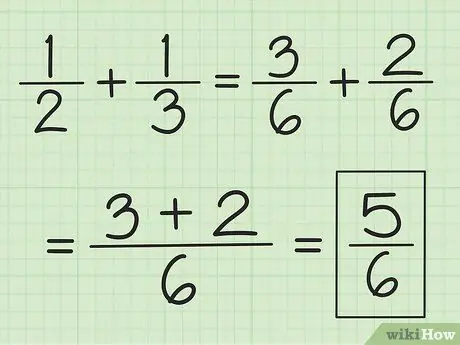
Krok 2. Sečtěte dva čitatele dohromady a neměňte jmenovatele
Například 3/6 plus 2/6 je 5/6 a 2/6 plus 1/6 je 3/6
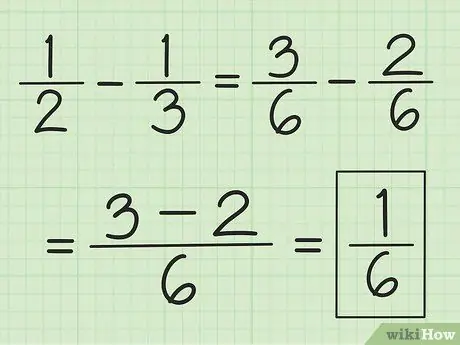
Krok 3. Pro odčítání použijte podobnou techniku
Nejprve najděte LCM jmenovatelů, ale místo jejich sčítání odečtěte číslo prvního čitatele od čísla druhého.
Chcete -li například odečíst 1/3 od 1/2, nejprve změňte zlomky na 3/6 a 2/6, poté odečtěte 3 od 2 a získáte 1. To má za následek 1/6
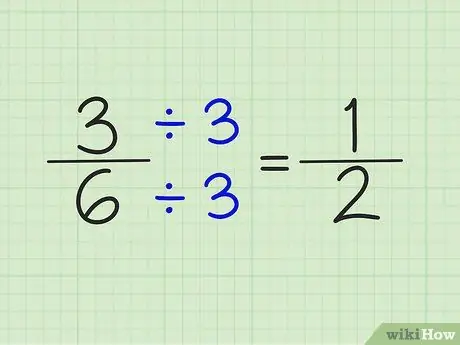
Krok 4. Zjednodušte zlomky vydělením čitatele a jmenovatele stejným číslem
Například číslo 5/6 nelze zjednodušit. 3/6 však lze zjednodušit vydělením čitatele a jmenovatele číslem 3. Výsledkem je zlomek 1/2

Krok 5. Převeďte zlomek na smíšené číslo, pokud je čitatel větší než jmenovatel
Metoda 4 z 5: Násobení a dělení zlomků
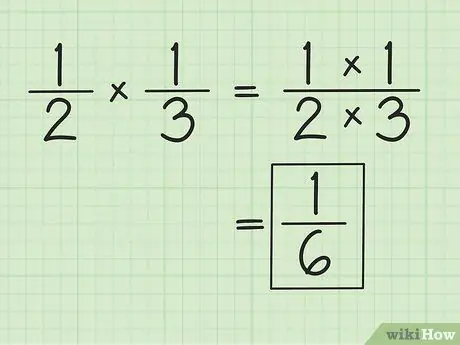
Krok 1. Násobením zlomku oddělte čitatele a jmenovatele samostatně
Například při násobení a 1/3 je výsledek 1/6 (1krát 1 a 2krát 3). Při násobení zlomků nemusíte spojovat jmenovatele. V případě potřeby získané výsledky zjednodušte nebo upravte
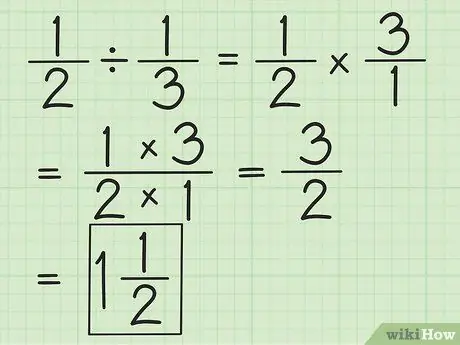
Krok 2. Rozdělte dvě frakce převrácením druhé frakce a poté obě vynásobte
Pokud například chcete dělit 1/2 na 1/3, nejprve otočte druhý zlomek na 3/1. Vynásobte 3/1 a získejte 3/2. Pokud je to možné, zjednodušte zlomky nebo převeďte na smíšená čísla
Metoda 5 z 5: Práce s komplexními zlomky
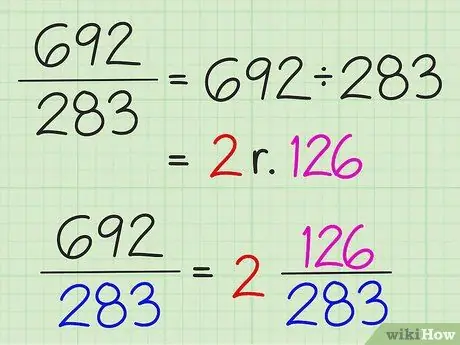
Krok 1. Zpracujte všechny zlomky stejným způsobem, i když se problém zdá velmi komplikovaný
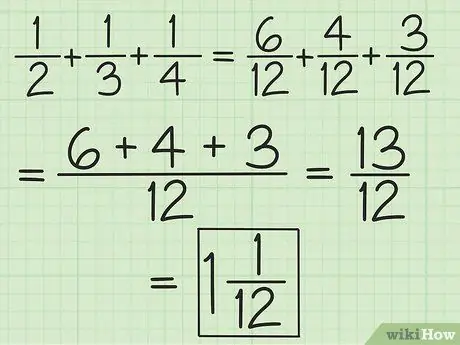
Krok 2. Porovnejte jmenovatele pro všechny zlomky nebo pracujte ve dvojicích zleva doprava a přidejte a odečtěte více než dvě zlomky
Chcete -li například sečíst 1/2, 1/3 a 1/4, můžete je změnit na 6/12, 4/12 a 3/12, abyste získali 13/12, nebo můžete přidat 3/6 a 2 /6, takže dostanete 5/6, pak přidejte 5/6 a 1/4 (vyrovnejte jmenovatele tak, aby se druhý zlomek stal 3/12), abyste získali 13/12 (10/12 plus 3/12). Převeďte jej na smíšené číslo, což je 1 1/12
Tipy
- Pamatujte, že jste se naučili hodně matematiky. Matematika je jako jazyk, který můžete plynule vyslovovat, a nyní se ji snažíte naučit číst a psát.
- Nezapomeňte vždy zjednodušit konečný výsledek výpočtu, ať už je váš problém ve formě obyčejného zlomku, smíšeného čísla nebo složitého zlomku.






