- Autor Jason Gerald [email protected].
- Public 2024-01-15 08:11.
- Naposledy změněno 2025-01-23 12:14.
Sčítání a odčítání zlomků je důležitá dovednost. Zlomky se v každodenním životě objevují neustále, zejména na hodinách matematiky, od základů po vysoké školy. Podle následujících kroků se naučíte, jak sčítat a odčítat zlomky, od ekvivalentních zlomků, nerovných zlomků, smíšených čísel nebo běžných zlomků. Pokud už znáte jeden způsob, je opravdu snadné vyřešit ostatní zlomky!
Krok
Metoda 1 ze 4: Sčítání a odčítání zlomků stejným jmenovatelem
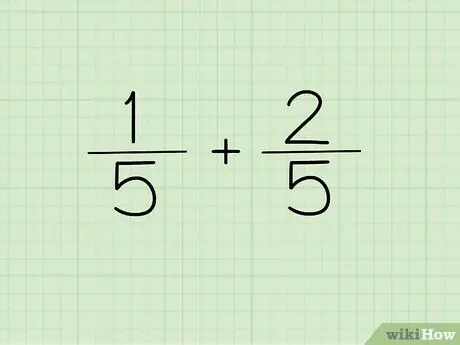
Krok 1. Zapište si otázku
Pokud je jmenovatel dvou zlomků, které chcete přidat nebo odečíst, stejný, zapište si jmenovatel jednou jako jmenovatele své odpovědi.
Jinými slovy, 1/5 a 2/5 nemusí být psáno jako 1/5 + 2/5 =?, ale lze jej zapsat jako (1+2)/5 =?. Jmenovatelé jsou stejní, takže je lze zapsat pouze jednou. Oba čitatelé jsou kombinováni
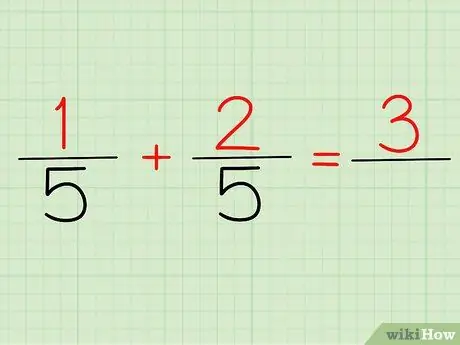
Krok 2. Sečtěte čitatele
Čitatel je číslo, které je nad libovolným zlomkem. Pokud se podíváme na výše uvedený problém, 1/5 a 2/5, 1 a 2 jsou naše čitatele.
Ať už to napíšete 1/5 + 2/5 nebo (1 + 2)/5, vaše odpověď bude stejná: 3! Protože 1 + 2 = 3

Krok 3. Opusťte jmenovatele
Jelikož jsou jmenovatelé stejní, nedělejte nic se jmenovateli! Nepřidávejte, neodečítejte, nerozmnožujte ani nedělejte. Nech to být.
Takže ze stejného příkladu je náš jmenovatel 5. Správně! 5 je spodní číslo našeho zlomku. Máme poloviční odpověď

Krok 4. Zapište si odpověď
Nyní si stačí zapsat svého čitatele a jmenovatele! Pokud použijete výše uvedený příklad, vaše odpověď bude 3/5.
Jaký je váš čitatel? 3. Váš jmenovatel? 5. Proto 1/5 + 2/5 nebo (1 + 2)/5 se rovná 3/5.
Metoda 2 ze 4: Sčítání a odčítání zlomků různými jmenovateli

Krok 1. Najděte nejméně společného jmenovatele
To znamená, že nejmenší jmenovatel je stejný pro obě zlomky. Předpokládejme, že máme zlomky 2/3 a 3/4. Co je jmenovatel? 3 a 4. Chcete -li najít nejmenšího společného jmenovatele obou zlomků, můžete to udělat třemi způsoby:
- Zapište si násobky. Násobky 3 jsou 3, 6, 9, 12, 15, 18… a tak dále. Násobky 4? 4, 8, 12, 16, 20 atd. Jaké je nejmenší číslo, které je násobkem těchto dvou? 12! To je nejmenší společný jmenovatel.
-
Prvočíselný rozklad. Pokud víte o faktorech, můžete provést primární faktorizaci. To znamená, že hledáte čísla, která tvoří vašeho jmenovatele. U čísla 3 jsou faktory 3 a 1. U čísla 4 jsou faktory 2 a 2. Potom vy všichni. 3 x 2 x 2 = 12. Váš nejmenší společný jmenovatel!
Vynásobte všechna čísla pro menší číslo. U některých problémů, jako je tento, můžete vynásobit obě čísla - 3 x 4 = 12. Pokud však máte velkého jmenovatele, nedělejte to! Nechcete znásobit 56 x 44 a jít naplno, abyste získali 2 464

Krok 2. Vynásobte jmenovatele číslem potřebným k získání nejmenšího společného jmenovatele
Jinými slovy, chcete, aby všichni vaši jmenovatelé byli stejní. V našem příkladu chceme, aby jmenovatel byl 12. Chcete -li změnit 3 na 12, vynásobte 3 krát 4. Chcete -li změnit 4 na 12, vynásobte 4 krát 3. Stejný jmenovatel bude jmenovatel vaší konečné odpovědi.
-
Takže 2/3 se stanou 2/3 x 4 a 3/4 se stanou 3/4 x 3. To znamená, že nyní máme 2/12 a 3/12. Ale ještě jsme neskončili!
- Všimnete si, že jmenovatelé se navzájem vynásobí. To lze v této situaci provést, ale ne ve všech situacích. Někdy místo vynásobení obou jmenovatelů můžete vynásobit oba jmenovatele jiným číslem, abyste získali menší číslo.
- Potom u dalších problémů někdy stačí znásobit jednoho jmenovatele, aby se rovnal jmenovateli druhého zlomku v problému.

Krok 3. Vynásobte čitatele stejným číslem
Když vynásobíte jmenovatele číslem, musíte také vynásobit čitatele stejným číslem. To, co jsme udělali v posledním kroku, je jen část násobení, které je třeba udělat.
Jako první krok máme 2/3x4 a 2/4x3 - pak ve druhém kroku 2 x 4/3 x 4 a 3 x 3/4 x 3. To znamená, že naše nová čísla jsou 8/12 a 9/ 12. Perfektní
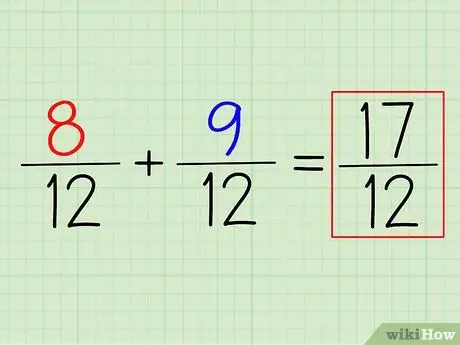
Krok 4. Přidáním (nebo odečtením) čitatelů získáte odpověď
Chcete -li přidat 8/12 + 9/12, stačí sečíst čitatele. Pamatujte: stačí nechat jmenovatele. Nejmenší společný jmenovatel, kterého najdete, je váš konečný jmenovatel.
V tomto případě (8+9)/12 = 17/12. Chcete -li jej převést na smíšené číslo, odečtěte jmenovatele od čitatele a zapište zbytek. V tomto případě 17/12 = 1 5/12
Metoda 3 ze 4: Sčítání a odčítání smíšených a běžných zlomků
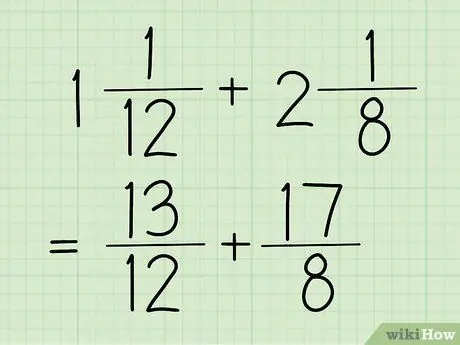
Krok 1. Převeďte své smíšené zlomky na běžné zlomky
Smíšené číslo je zlomek, který má celé číslo a zlomek, jako v příkladu výše (1 5/12). Mezitím je obyčejný zlomek zlomek, jehož čitatel (horní číslo) je větší než jmenovatel (spodní číslo). Tato frakce je také vidět v předchozím kroku, který je 17/12.
Pro příklady v této části použijeme 13/12 a 17/8

Krok 2. Najděte společného jmenovatele
Pamatujete si tři způsoby, jak najít nejméně společného jmenovatele? Napsáním násobků, použitím primární faktorizace nebo vynásobením jmenovatelů.
Pojďme najít násobky našeho příkladu, 12 a 8. Jaké je nejmenší číslo, které mají oba společné? 24. 8, 16, 24 a 12, 24 - bingo

Krok 3. Vynásobením svého čitatele a jmenovatele najdete ekvivalentní zlomek
Oba jmenovatele je třeba změnit na 24. Jak převedete 12 na 24? Násobit 2. 8 až 24? Vynásobte třemi. Ale nezapomeňte - musíte také znásobit čitatele!
Takže (13 x 2)/(12 x 2) = 26/24. A (17 x 3)/(8 x 3) = 51/24. Už jsme z toho skoro hotovi

Krok 4. Sečtěte nebo odečtěte své zlomky
Nyní, když máte stejného jmenovatele, můžete tyto dva čitatele snadno sčítat. Nezapomeňte, ponechte jmenovatele!
26/24 + 51/24 = 77/24. To je vaše částka! Čísla nahoře však byla příliš velká …

Krok 5. Převeďte svou odpověď zpět na smíšená čísla
Velmi velké číslo v horní části zlomku působí trochu zvláštně - nemůžete určit velikost zlomku. Jediné, co musíte udělat, je odečíst svého jmenovatele od čitatele opakovaně, dokud jej již nelze odečíst a zapsat zbytek.
-
V tomto případě 77 minus 24 krát 3krát. To znamená, že 24 x 3 = 72. Zbytek je 5! Jaký je tedy váš konečný výsledek? 3 5/24.
Tak pravdivé!
Metoda 4 ze 4: Sčítání a odčítání zlomků bez nalezení LCM
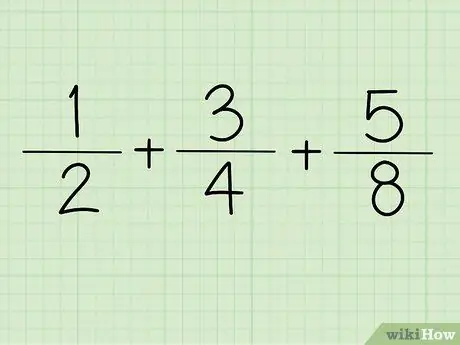
Krok 1. Zapište si zlomek
Například + +

Krok 2. Vyřešte nejprve čitatele
- Vynásobte čitatelem druhého zlomku.
- Vynásobte 1 číslicemi 4 a 8. [32]
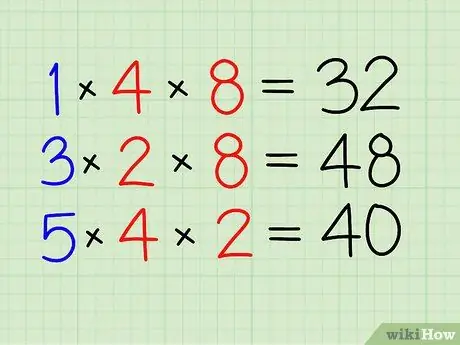
Krok 3. Totéž proveďte pro ostatní frakce
- Vynásobte 3 číslicemi 2 a 8. [48]
- Nakonec vynásobte 5 číslicemi 4 a 2. [40]
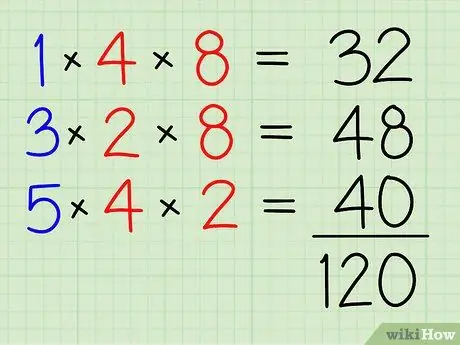
Krok 4. Přidejte je všechny dohromady
32+48+40=120
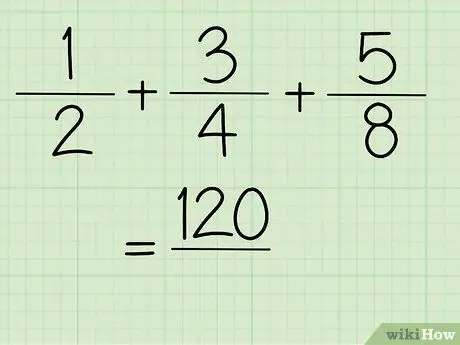
Krok 5. Nyní získáte hodnotu čitatele

Krok 6. Vyřešte jmenovatele zlomku

Krok 7. Vynásobte všechny jmenovatele zlomků
2×4×8=64

Krok 8. Nyní získáte výsledek
120/64 = 1 56/64 = 1 ⅞
Varování
- Tato metoda umožňuje znásobit velká čísla.
- K tomuto způsobu výpočtu budete možná potřebovat kalkulačku.






