Geometrický průměr je dalším způsobem nalezení průměrné hodnoty sady čísel, který se provádí vynásobením hodnot před převzetím kořenů, místo sčítání hodnot a jejich dělení jako v aritmetickém průměru. Geometrický průměr lze použít k výpočtu průměrné míry návratnosti ve finanční analýze nebo k zobrazení rychlosti růstu něčeho za určité časové období. Chcete -li zjistit geometrický průměr, vynásobte všechny hodnoty před rootováním, což je celkový počet čísel v sadě. Pokud chcete, můžete také použít funkci logaritmu ve své kalkulačce k nalezení geometrického průměru.
Krok
Metoda 1 ze 2: Nalezení geometrického průměru sady hodnot
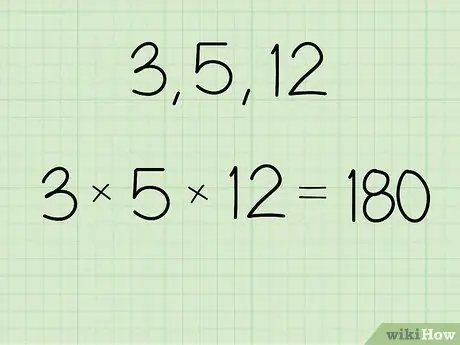
Krok 1. Vynásobte hodnotu, pro kterou chcete zjistit geometrický průměr
K získání výsledku můžete použít kalkulačku nebo vypočítat ručně. Zapište si výsledky, abyste nezapomněli.
- Pokud je například sada čísel 3, 5 a 12, vypočítejte: (3 x 5 x 12) = 180.
- Pro další příklad, pokud chcete najít geometrický průměr množiny čísel 2 a 18, napište: (2 x 18) = 36.
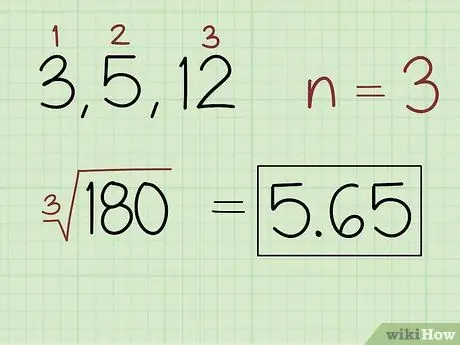
Krok 2. Najděte n -tý kořen součinu, kde n je počet hodnot v sadě
Spočítejte počet čísel v sadě, abyste získali hodnotu. Pomocí hodnot určete kořen, který je třeba v produktu použít. Například použijte odmocninu, pokud sada obsahuje 2 čísla, krychlovou odmocninu, pokud sada obsahuje 3 čísla atd. Pomocí kalkulačky vyřešte rovnici a napište odpověď.
- Například pro sadu čísel 3, 5 a 12 napište: (180) 5, 65.
- Do druhého příkladu se sadou obsahující 2 a 18 napište: (36) = 6.
Variace:
Kořen můžete také napsat jako exponent 1/, pokud je jednodušší psát na kalkulačce. Například pro množinu čísel 3, 5 a 12 napište (180)1/3 místo (180).
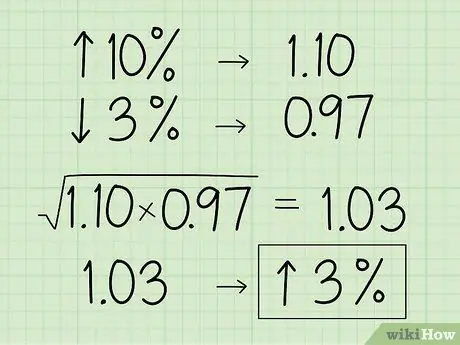
Krok 3. Převeďte procento na ekvivalent jeho desetinného multiplikátoru
Pokud je sada čísel zapsána jako zvýšení nebo snížení v procentech, zkuste nepoužívat procentní hodnotu v geometrickém průměru, protože výsledky nebudou přesné. Pokud se procento zvyšuje, přesuňte desetinnou čárku o dvě číslice doleva a přidejte 1. Pokud se procento snižuje, přesuňte desetinnou čárku o 2 číslice doleva a odečtěte od 1.
- Řekněme například, že chcete najít geometrický průměr hodnot objektu, který se zvýší o 10%a poté se sníží o 3%.
- Převeďte 10% na desetinné číslo a přidáním 1 získáte 1, 10.
- Poté převeďte 3% na desetinné číslo a odečtěte 1, abyste získali 0,97.
- K nalezení geometrického průměru použijte obě desetinná místa: (1, 10 x 0,97) 1,03.
- Převeďte číslo zpět na procento posunutím desetinné čárky o 2 číslice doprava a odečtením 1 získáte 3% nárůst hodnoty.
Metoda 2 ze 2: Výpočet geometrického průměru pomocí logaritmů
Krok 1. Sečtěte logaritmické hodnoty pro každé číslo v sadě
Funkce LOG v kalkulačce vezme základnu 10 čísla a určí, kolik potřebujete vynásobit 10, aby se rovnalo číslu. Vyhledejte funkci LOG na kalkulačce, která je obvykle na levé straně tlačítka. Klikněte na tlačítko LOG a zadejte první číslo v sadě. Před zadáním LOG pro druhé číslo zadejte „+“. Před získáním součtu pokračujte v oddělení funkce LOG pro každé číslo symbolem plus.
- Například pro sady 7, 9 a 12 zadejte log (7) + log (9) + log (12) a poté na kalkulačce stiskněte „=“. Pokud byla funkce vypočítána, bude se číslo pohybovat kolem 2,878521796.
- Každý logaritmus můžete také vypočítat samostatně, než je všechny sečtete.
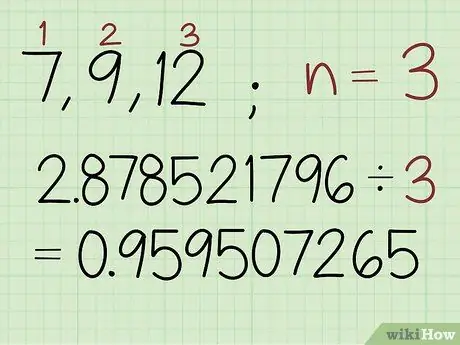
Krok 2. Vydělte součet logaritmických hodnot počtem čísel v sadě
Spočítejte počet hodnot v sadě a vydělte dříve získané číslo tímto číslem. Výsledkem je logaritmus geometrického průměru.
V tomto příkladu jsou v sadě 3 čísla, takže zadejte: 2, 878521796 /3 0, 959507265
Krok 3. Najděte antilog kvocientu pro určení geometrického průměru
Funkce antilog je inverzní funkcí LOG na kalkulačce a převádí hodnotu zpět na základnu 10. Vyhledejte symbol „10X”Na kalkulačce, což je obvykle sekundární funkce tlačítka LOG. Stisknutím tlačítka „2nd“v levém horním rohu kalkulačky a následně tlačítka LOG aktivujte funkci Antilog. Před vyřešením rovnice zadejte kvocient nalezený v posledním kroku.
V tomto případě kalkulačka zobrazí: 10(0, 959507265) ≈ 9, 11.
Tipy
- Nemůžete najít geometrický průměr záporných čísel.
- Všechny sady, které mají 0, budou mít geometrický průměr 0.
